题目内容
16.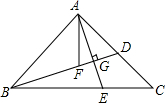 如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.
如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.
分析 由直角三角形的两个锐角互余得出∠ABF=∠CAE,再由等腰直角三角形的性质和角平分线得出∠BAF=∠C,由ASA证明△BAF≌△CAE,得出对应边相等即可.
解答 证明:∵∠BAC=90°,AE⊥BD,
∴∠CAE+∠BAE=∠ABF+∠BAE=90°,
∴∠ABF=∠CAE,
∵AB=AC,∠BAC=90°,AF是角平分线,
∴∠BAF=45°=∠C,
在△BAF和△CAE中,$\left\{\begin{array}{l}{∠ABF=∠CAE}&{\;}\\{AB=AC}&{\;}\\{∠BAF=∠C}&{\;}\end{array}\right.$,
∴△BAF≌△CAE(ASA),
∴AE=BF.
点评 本题考查了等腰直角三角形的性质、直角三角形两个锐角互余的性质、全等三角形的判定与性质;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
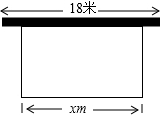 学校准备在图书馆后面的场地边建一个矩形自行车棚,一边利用图书馆的后墙,(已知后墙长18米),另三边利用总长为25米的铁围栏围成.
学校准备在图书馆后面的场地边建一个矩形自行车棚,一边利用图书馆的后墙,(已知后墙长18米),另三边利用总长为25米的铁围栏围成.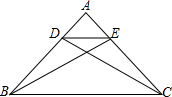 如图,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC于点E,求证:DE∥BC.
如图,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC于点E,求证:DE∥BC. ( )
( )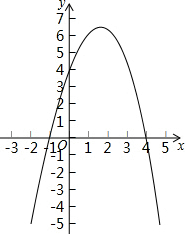 已知二次函数y=-x2+3x+4的图象如图:(直接写答案)
已知二次函数y=-x2+3x+4的图象如图:(直接写答案)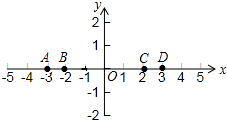 如图所示,C,D两点的横坐标分别为2,3.线段CD=1;B,D两点的横坐标分别为-2,3.线段BD=5;A,B两点的横坐标分别为-3,-2,线段AB=1,请探究:
如图所示,C,D两点的横坐标分别为2,3.线段CD=1;B,D两点的横坐标分别为-2,3.线段BD=5;A,B两点的横坐标分别为-3,-2,线段AB=1,请探究: