在平面直角坐标系中.已知点A与点B关于原点对称.则a=2.b=2．题目和参考答案——青夏教育精英家教网——

题目内容

9．在平面直角坐标系中，已知点A（2a-b，-8）与点B（-2，a+3b）关于原点对称，则a=2，b=2．

分析利用关于原点对称的点的特点建立方程组即可．

解答解：∵点A（2a-b，-8）与点B（-2，a+3b）关于原点对称，
∴2a-b=2，a+3b=8，
∴a=2，b=2，
故答案为2，2．

点评此题是关于原点对称的点的坐标，主要考查坐标系中点的对称点的特征，熟记对称点的特征是解本题的关键，是一道简单题．

练习册系列答案

金点新课标同步精练系列答案

教材精析精练字词句篇系列答案

上海中考总动员系列答案

春雨教育同步作文系列答案

新课标应用题系列答案

通城学典拓展阅读训练系列答案

单元自测试卷青岛出版社系列答案

天利38套小升初特训卷系列答案

时事政治系列答案

全效学习中考学练测系列答案

相关题目

20．几位同学尝试用矩形纸条ABCD（如图1）折出常见的中心对称图形．

（1）如图2，小明将矩形纸条先对折，使AB和DC重合，展开后得折痕EF，再折出四边形ABEF和CDEF的对角线，它们的对角线分别相交于点G，H，最后将纸片展平，则四边形EGFH的形状一定是菱形．
（2）如图3，小华将矩形纸片沿EF翻折，使点C，D分别落在矩形外部的点C′，D′处，FC′与AD交于点G，延长D′E交BC于点H，求证：四边形EGFH是菱形．
（3）如图4，小美将矩形纸条两端向中间翻折，使得点A，C落在矩形内部的点A′，C′处，点B，D落在矩形外部的点B′，D′处，折痕分别为EF，GH，且点H，C′，A′，F在同一条直线上，试判断四边形EFGH的形状，并说明理由．

1．先化简，再求值：
（（2x+y）²-y（y+4x）-8xy）÷2x，其中x=$\frac{1}{2}$，y=-1．

17．把方程$\frac{1}{3}$x²-x-5=0，化成（x+m）²=n的形式得（　　）

（x-$\frac{3}{2}$）²=$\frac{29}{4}$

（x-$\frac{3}{2}$）²=$\frac{27}{2}$

（x-$\frac{3}{2}$）²=$\frac{51}{4}$

（x-$\frac{3}{2}$）²=$\frac{69}{4}$

4．下列计算正确的是（　　）

$\sqrt{4+9}=\sqrt{4}+\sqrt{9}$

2$\sqrt{2}-\sqrt{2}$=2

$\sqrt{2}×\sqrt{3}=\sqrt{5}$

$\frac{{\sqrt{21}}}{{\sqrt{3}}}=\sqrt{\frac{21}{3}}=\sqrt{7}$

如图，AB∥CD，AF平分∠BAC，且交CD于点E，若∠CEA=27°，则∠DCG的度数为　（　　）

1．计算：
（1）$-\sqrt{7}÷3\sqrt{\frac{14}{15}}×\frac{3}{2}\sqrt{2\frac{1}{2}}$
（2）$2\sqrt{x{y^3}}÷（{-\frac{1}{2}\sqrt{{x^3}{y^2}}}）$
（3）$\sqrt{4\frac{4}{5}}•3\sqrt{5}÷（-\frac{3}{4}\sqrt{10}）$
（4）$\sqrt{a{b^3}}÷（{-3\sqrt{\frac{b}{2a}}}）×（{-3\sqrt{2a}}）$
（5）$\sqrt{24}+\sqrt{\frac{2}{3}}-3\sqrt{6}$
（6）$\sqrt{30}×\frac{3}{2}\sqrt{2\frac{2}{3}}÷2\sqrt{2\frac{1}{2}}$
（7）${（{\sqrt{5}-2}）^2}+（{\sqrt{5}-3}）（{\sqrt{5}+3}）$
（8）$（\frac{1}{3}\sqrt{27}-\sqrt{24}-3\sqrt{\frac{2}{3}}）•\sqrt{12}$．

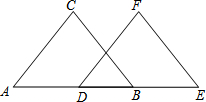看图填空：已知，如图，BC∥EF，AD=BE，BC=EF．试说明△ABC≌△DEF
解：∵AD=BE
∴AD+DB=BE+DB；　　即：AB=DE
∵BC∥EF
∴∠ABC=∠E（两直线平行，同位角相等）
在△ABC和△DEF中，BC=EF，∠ABC=∠E，AB=DE，
∴△ABC≌△DEF （SAS）．

如图，在△ABC中，BC=5，AC=8，AB的垂直平分线交AB于点D，交AC于点E，则△BCE的周长为（　　）