题目内容
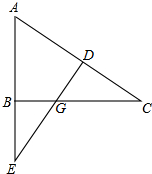 已知:如图,∠ABC=90°,DE⊥AC于点D,交BC于点G,交AB的延长线于点E,且AE=AC.求证:
已知:如图,∠ABC=90°,DE⊥AC于点D,交BC于点G,交AB的延长线于点E,且AE=AC.求证:(1)AB=AF;
(2)BG=DG.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)根据AAS,可得△ABC和△ADE的关系,再根据全等三角形的性质,可得答案;
(2)根据HL,可得△ABG与△ADG的关系,再根据全等三角形的性质,可得答案.
(2)根据HL,可得△ABG与△ADG的关系,再根据全等三角形的性质,可得答案.
解答:证明:(1)在△ABC和△ADE中
,
∴△ABC≌△ADE(AAS),
∴AB=AD;
(2)连接AG ,
,
在Rt△ABG与Rt△ADG中
,
∴△ABG≌△ADG(HL),
∴BG=DG.
|
∴△ABC≌△ADE(AAS),
∴AB=AD;
(2)连接AG
 ,
,在Rt△ABG与Rt△ADG中
|
∴△ABG≌△ADG(HL),
∴BG=DG.
点评:本题考查了全等三角形的判定与性质,(1)利用了AAS证明三角形全等,(2)利用了HL证明两个三角形全等.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,数轴上A点表示的数可能是( )
如图,数轴上A点表示的数可能是( )A、
| ||
B、
| ||
C、
| ||
D、
|
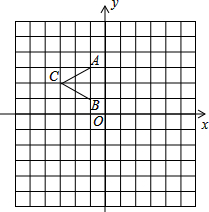 如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)
如图,△ABC三个顶点坐标分别为A(-1,3),B(-1,1),C(-3,2)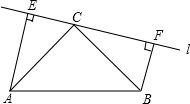 如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足为E,F.
如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,垂足为E,F.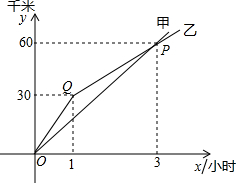 自行车运动员甲、乙在公路上进行训练.如图,是反映他们在训练过程中的行驶路程(千米)和行驶时间(小时)之间的部分图象.
自行车运动员甲、乙在公路上进行训练.如图,是反映他们在训练过程中的行驶路程(千米)和行驶时间(小时)之间的部分图象.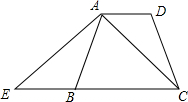 如图,在四边形ABCD中,AD∥BC,且AB=CD,∠D=∠BAD,延长线段CB到E,使BE=AD,连接AE、AC
如图,在四边形ABCD中,AD∥BC,且AB=CD,∠D=∠BAD,延长线段CB到E,使BE=AD,连接AE、AC 如图,AB是⊙O的直径,弦CD⊥AB,交AB于点E,∠CDB=30°,⊙O的半径为2cm,求弦CD的长.
如图,AB是⊙O的直径,弦CD⊥AB,交AB于点E,∠CDB=30°,⊙O的半径为2cm,求弦CD的长.