题目内容
下列条件①∠A：∠B：∠C=1：2：3；②a：b：c=3：4：5；③a=3，b=4，c=5；④c2-a2=b2，其中能使△ABC是直角三角形的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
考点：勾股定理的逆定理,三角形内角和定理
专题：
分析：分别根据三角形内角和定理、勾股定理的逆定理对各选项进行逐一分析即可．
解答：解：①∵∠A：∠B：∠C=1：2：3，
∴设∠A=x，则∠B=2x，∠C=3x．
∵∠A+∠B+∠C=180°，
∴x+2x+3x=180°，解得x=30°，
∴∠C=3x=90°，
∴此三角形是直角三角形，故本小题正确；
②∵a：b：c=3：4：5，
∴设a=3x，则b=4x，c=5x，
∵（3x）2+（4x）2=（5x）2，
∴此三角形是直角三角形，故本小题正确；
③∵a=3，b=4，c=5，32+42=52，
∴此三角形是直角三角形，故本小题正确；
④∵c2-a2=b2，
∴b2+a2=c2，
∴此三角形是直角三角形，故本小题正确．
故选D．
∴设∠A=x，则∠B=2x，∠C=3x．
∵∠A+∠B+∠C=180°，
∴x+2x+3x=180°，解得x=30°，
∴∠C=3x=90°，
∴此三角形是直角三角形，故本小题正确；
②∵a：b：c=3：4：5，
∴设a=3x，则b=4x，c=5x，
∵（3x）2+（4x）2=（5x）2，
∴此三角形是直角三角形，故本小题正确；
③∵a=3，b=4，c=5，32+42=52，
∴此三角形是直角三角形，故本小题正确；
④∵c2-a2=b2，
∴b2+a2=c2，
∴此三角形是直角三角形，故本小题正确．
故选D．
点评：本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．
练习册系列答案
相关题目
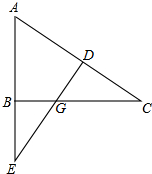已知：如图，∠ABC=90°，DE⊥AC于点D，交BC于点G，交AB的延长线于点E，且AE=AC．求证：
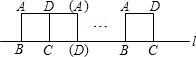将边长为4cm的正方形ABCD的四边沿直线l向右滚动（不滑动），当正方形滚动两周时，正方形的顶点A所经过的路线的长是
如图所示，抛物线y=-（x-1）2+4与x轴交于A、B两点，与y轴交于C点，顶点为D．若抛物线上有一点P（点P不与点C重合），使得S△DCB=S△PCB，则这样的点P总共存在
小亮家里装修房子，爸爸想考一考他，爸爸拿出一块四条边都是80cm的瓷砖（瓷砖的平面图如图所示），要求他检验一下四个角是否为直角，能用的工具只有10cm的一段直尺，如果你是小亮，你认为能完成吗？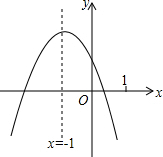
二次函数y=ax2+bx+c（a≠0）的图象如图所示：则下列结论：①abc＞0；②b-2a=0；③a+b+c＞0；④b2-4ac＞0；正确的有（ ）下列运算正确的是（ ）
| A、a5•a2=a10 |
| B、（x2）3=x6 |
| C、x3+x7=x10 |
| D、（-ab）6÷（-ab）2=a3b3 |
若抛物线y=-x2-2x+c的图象经过点A（-2，y1）、B（1，y2），则y1与y2的大小关系是（ ）
| A、y1＜y2 |
| B、y1＞y2 |
| C、y1=y2 |
| D、无法判断 |
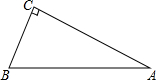在△ABC中，∠ACB=90°，AC=4，BC=2，以AB为边向外作等腰直角三角形ABD，求CD的长．