题目内容
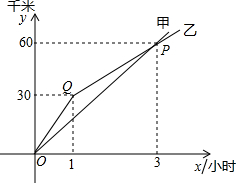 自行车运动员甲、乙在公路上进行训练.如图,是反映他们在训练过程中的行驶路程(千米)和行驶时间(小时)之间的部分图象.
自行车运动员甲、乙在公路上进行训练.如图,是反映他们在训练过程中的行驶路程(千米)和行驶时间(小时)之间的部分图象.(1)点P是两条线的一个交点,由此可以得到什么?
(2)在哪一段时间,乙的行驶的速度大于甲的行驶的速度?
(3)若甲的行驶速度不变,乙在行驶了4小时后,需要使行驶速度达到多少时,才能够在100千米处追上甲.
考点:一次函数的应用
专题:
分析:(1)观察图象即可得出P点表示的实际意义;
(2)由图象观察可以得出,出发3小时后甲的速度大于乙的速度,在出发3小时内相同的时间乙走的路程多可以求出结论;
(3)求出PQ的解析式,求出4小时时甲、乙行驶的路程,根据追击问题建立方程求出其解就可以了.
(2)由图象观察可以得出,出发3小时后甲的速度大于乙的速度,在出发3小时内相同的时间乙走的路程多可以求出结论;
(3)求出PQ的解析式,求出4小时时甲、乙行驶的路程,根据追击问题建立方程求出其解就可以了.
解答:解:(1)由图象观察可以得:P点是两个图象的交点,表示甲、乙相遇的时候甲、乙行驶的路程都是60千米,行驶的时间都是3小时;
(2)通过图象观察得出:在出发3小时内乙的行驶的速度大于甲的行驶的速度;
(3)设直线PQ的解析式为:y=kx+b,由图象得:
,
解得:
,
故直线PQ的解析式为:y=15x+15.
当x=4时,
乙行驶的路程为:y=4×15+15=75,
甲行驶的路程为:20×4=80.
设乙的速度达到m千米/时,就可以在100千米处追上甲,由题意得:
=
,
解得:m=25.
故乙的速度达到25千米/时,就可以在100千米处追上甲.
(2)通过图象观察得出:在出发3小时内乙的行驶的速度大于甲的行驶的速度;
(3)设直线PQ的解析式为:y=kx+b,由图象得:
|
解得:
|
故直线PQ的解析式为:y=15x+15.
当x=4时,
乙行驶的路程为:y=4×15+15=75,
甲行驶的路程为:20×4=80.
设乙的速度达到m千米/时,就可以在100千米处追上甲,由题意得:
| 25 |
| m |
| 20 |
| 20 |
解得:m=25.
故乙的速度达到25千米/时,就可以在100千米处追上甲.
点评:本题考查了一次函数的图象运用,解答问题的关键是读懂图象所表示的实际意义,运用待定系数法求出函数解析式.

练习册系列答案
相关题目
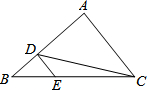 如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE:S△CDE=1:3,则S△BDE:S△ACD=( )
如图,在△ABC中,D,E分别是AB,BC上的点,且DE∥AC,若S△BDE:S△CDE=1:3,则S△BDE:S△ACD=( )| A、1:5 | B、1:9 |
| C、1:10 | D、1:12 |
 如图,等边△ABC中,高AD、BE相交于F点,则图中等腰三角形的个数(除△ABC外)是( )
如图,等边△ABC中,高AD、BE相交于F点,则图中等腰三角形的个数(除△ABC外)是( )| A、5 | B、6 | C、7 | D、8 |
 如图,数轴上的点P表示的数可能是( )
如图,数轴上的点P表示的数可能是( )| A、-3.7 | ||
B、
| ||
C、-
| ||
D、-
|
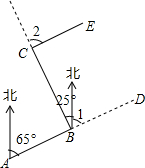 林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?
林湾乡修建一条灌溉水渠,如图,水渠从A村沿北偏东65°方向到B村,从B村沿北偏西25°方向到C村水渠从C村沿什么方向修建,可以保持与AB的方向一致?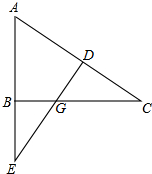 已知:如图,∠ABC=90°,DE⊥AC于点D,交BC于点G,交AB的延长线于点E,且AE=AC.求证:
已知:如图,∠ABC=90°,DE⊥AC于点D,交BC于点G,交AB的延长线于点E,且AE=AC.求证: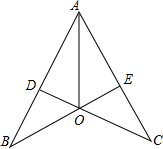 如图:AB=AC,BD=CE.求证:OA平分∠BAC.
如图:AB=AC,BD=CE.求证:OA平分∠BAC. 小亮家里装修房子,爸爸想考一考他,爸爸拿出一块四条边都是80cm的瓷砖(瓷砖的平面图如图所示),要求他检验一下四个角是否为直角,能用的工具只有10cm的一段直尺,如果你是小亮,你认为能完成吗?
小亮家里装修房子,爸爸想考一考他,爸爸拿出一块四条边都是80cm的瓷砖(瓷砖的平面图如图所示),要求他检验一下四个角是否为直角,能用的工具只有10cm的一段直尺,如果你是小亮,你认为能完成吗?