题目内容
6.已知A(-2,0)、B(-4,5),在x轴上求作一点C,使SCABC=6.分析 由三角形的面积为6可确定出底边AC的长,然后再确定出点C的坐标即可.
解答 解:∵SCABC=6,
∴$\frac{1}{2}×5×AC=6$.
∴AC=$\frac{12}{5}$.
-2+$\frac{12}{5}$=$\frac{2}{5}$,-2-$\frac{12}{5}$=-$\frac{22}{5}$.
所以点C的坐标为($\frac{2}{5}$,0)或($-\frac{22}{5}$,0).
点评 本题主要考查的是坐标与图形的性质,根据三角形的面积求得AC的长是解题的关键.

练习册系列答案
相关题目
16.方程2x2-4x+1=0的根是( )
| A. | x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$ | B. | x1=2+2$\sqrt{2}$,x2=2-2$\sqrt{2}$ | C. | x1=1+$\frac{\sqrt{2}}{2}$,x2=1-$\frac{\sqrt{2}}{2}$ | D. | x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$ |
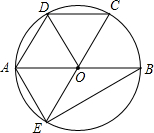 如图,AB,CE是⊙O的直径,∠COD=60°,且$\widehat{AD}$=$\widehat{BC}$.
如图,AB,CE是⊙O的直径,∠COD=60°,且$\widehat{AD}$=$\widehat{BC}$.