题目内容
14.已知⊙O的半径为10cm,AB为直径,CD为弦,CD⊥AB,垂足为E,若CD=12cm,求AE的长.分析 根据垂径定理求得CE的长,然后根据勾股定理求得OE的长,即可求得AE的长.
解答  解:∵AB为直径,CD为弦,CD⊥AB,
解:∵AB为直径,CD为弦,CD⊥AB,
∴CE=DE=$\frac{1}{2}$CD=6cm,
连接OC,
∴OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8cm,
∴AE=10+8=18cm或AE=10-8=2cm;
∴AE的长为18cm或2cm.
点评 本题考查的是垂径定理和勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
5.如图,是一个简单的数值运算程序.则输入x的值为( )

| A. | 3或-3 | B. | 4或-2 | C. | 1或3 | D. | 27 |
3.若3xayb+3与7x2-3bya+1是同类项,则a,b的值分别是( )
| A. | a=0,b=2 | B. | a=-2,b=0 | C. | a=2,b=0 | D. | a=0,b=-2 |
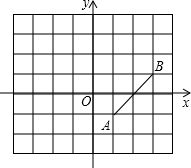 如图,线段AB两个端点的坐标分别为A(1,-1),B(3,1),将线段AB绕点O逆时针旋转90°到对应线段CD(点A与点C对应,点B与D对应).
如图,线段AB两个端点的坐标分别为A(1,-1),B(3,1),将线段AB绕点O逆时针旋转90°到对应线段CD(点A与点C对应,点B与D对应).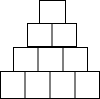 用若干个小立方块搭成的一个四层塔体的主视图,左视图是相同的图形,如图所示:
用若干个小立方块搭成的一个四层塔体的主视图,左视图是相同的图形,如图所示: