题目内容
如图，?ABCD中，BD是对角线，AE⊥BD于E，CF⊥BD于F．若∠ABE=47°，求∠DCF．考点：平行四边形的性质
专题：
分析：首先根据平行四边形对边平行可得∠ABE=∠BDC=47°，再根据直角三角形两锐角互余可得答案．
解答：解：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠ABE=∠BDC=47°，
∵CF⊥BD于F，
∴∠CFD=90°，
∴∠DCF=90°-47°=43°．
∴AB∥CD，
∴∠ABE=∠BDC=47°，
∵CF⊥BD于F，
∴∠CFD=90°，
∴∠DCF=90°-47°=43°．
点评：此题主要考查了平行四边形的性质，以及直角三角形的性质，关键是掌握平行四边形对边平行．
练习册系列答案
相关题目
如图，正方形的边长为a，剪去四个角后成为一个正八边形，则这个正八边形的边长为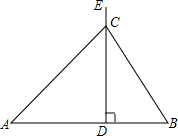
如图，线段AB=a，在垂直于AB的射线DE上有一个动点C（C与D不重合），分别联结CA、CB，得到△ABC．
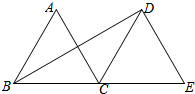如图，△ABC和△DCE都是边长为4的等边三角形，点B、C、E在同一条直线上，连接BD，则BD的长为