题目内容
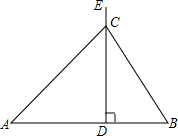 如图,线段AB=a,在垂直于AB的射线DE上有一个动点C(C与D不重合),分别联结CA、CB,得到△ABC.
如图,线段AB=a,在垂直于AB的射线DE上有一个动点C(C与D不重合),分别联结CA、CB,得到△ABC.(1)指出△ABC的面积的变化过程中,线段AB、CD的长哪个是常量?哪个是变量?
(2)设CD的长为h,△ABC的面积为S,S是不是h的函数?
考点:函数的概念,常量与变量
专题:
分析:(1)根据题意知道AB的长度不变,CD的长度随着点C位置的变化而变化;
(2)由三角形的面积公式列出函数关系式,根据函数的概念进行判断.
(2)由三角形的面积公式列出函数关系式,根据函数的概念进行判断.
解答:解:(1)依题意知,AB是常量,CD是变量;
(2)S=
AB•CD=
AB•h,即S=
AB•h.
因为在S的过程中有两个变量S与h,对于h的每一个确定的值,S都有唯一的值与其对应,所以说S是h的函数.
(2)S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因为在S的过程中有两个变量S与h,对于h的每一个确定的值,S都有唯一的值与其对应,所以说S是h的函数.
点评:本题考查了函数的概念和变量与常量.对于函数概念的理解:
①有两个变量;
②一个变量的数值随着另一个变量的数值的变化而发生变化;
③对于自变量的每一个确定的值,函数值有且只有一个值与之对应,即单对应.
①有两个变量;
②一个变量的数值随着另一个变量的数值的变化而发生变化;
③对于自变量的每一个确定的值,函数值有且只有一个值与之对应,即单对应.

练习册系列答案
相关题目
 如图所示,某市为加固长为10m,高为5m,坝顶宽为4m,迎水坡和背水坡的坡度都是1:1,横断面都是梯形的防洪大坝,现要将大坝加高1m,背水坡坡度改为1:2,已知迎水坡度不变,坝顶宽度不变.
如图所示,某市为加固长为10m,高为5m,坝顶宽为4m,迎水坡和背水坡的坡度都是1:1,横断面都是梯形的防洪大坝,现要将大坝加高1m,背水坡坡度改为1:2,已知迎水坡度不变,坝顶宽度不变.  如图,?ABCD中,BD是对角线,AE⊥BD于E,CF⊥BD于F.若∠ABE=47°,求∠DCF.
如图,?ABCD中,BD是对角线,AE⊥BD于E,CF⊥BD于F.若∠ABE=47°,求∠DCF.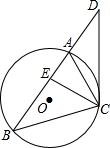 如图,已知CD是△ABC的外接圆的切线,C为切点,BA的延长线与切线CD相交于点D,点E在边AB上,且DE=DC.求证:CE平分∠ACB.
如图,已知CD是△ABC的外接圆的切线,C为切点,BA的延长线与切线CD相交于点D,点E在边AB上,且DE=DC.求证:CE平分∠ACB.