题目内容
11.已知平行四边形ABCD中,(1)如图1,若DE=BF,求证:四边形AFCE是平行四边形;
(2)若AE、CF分别是∠DAB,∠BCD的平分线,求证:四边形AFCE是平行四边形;
(3)如图2,在(1)的基础上,连接BE,DF,分别交FC,EA于点G,H.求证:四边形EHFG为平行四边形.

分析 (1)根据平行四边形的对边相等得AB=CD,已知DE=BF,再作线段的差可得CE=AF,即可得出结论;
(2)证出AE∥CF,可证四边形AFCE是平行四边形;
(3)由(1)得:四边形AFCE是平行四边形,得出AF=CE,证出BF=DE,得出四边形BEDF为平行四边形,得出DF∥BE,即可得出结论.
解答 (1)证明:∵四边形ABCD为平行四边形,
∴AB=CD.AB∥CD,
又∵DE=BF,
∴AB-BF=CD-DE.即AF=CE,
∴四边形AFCE是平行四边形.
(2)证明:∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,AB∥CD,
∴∠BAE=∠DEA,
∵AE、CF分别是∠DAB,∠BCD的平分线,
∴∠BAE=∠DCF,
∴∠DEA=∠DCF,
∴AE∥CF,
∴四边形AFCE是平行四边形.
(3)证明:由(1)得:四边形AFCE是平行四边形,
∴AF=CE,AE∥CF,
∵AB=CD,
∴BF=DE,
又∵AB∥CD,
∴四边形BEDF为平行四边形,
∴DF∥BE,
∴四边形EHFG为平行四边形.
点评 本题考查了平行四边形的性质及判定方法.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.

练习册系列答案
相关题目
19.下列说法中,正确的是( )
| A. | 为检测市场上正在销售的酸奶质量,应该采用全面调查的方式 | |
| B. | 在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 | |
| C. | 小强班上有3个同学都是16岁,因此小强认为他们班学生年龄的众数是16岁 | |
| D. | 给定一组数据,则这组数据的中位数一定只有一个 |
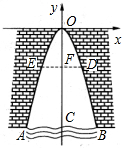 某涵洞的截面边缘成抛物线形,现测得当水面宽AB=2米时涵洞的顶点与水面的距离为4米,这时离开水面2米处涵洞宽DE是多少?
某涵洞的截面边缘成抛物线形,现测得当水面宽AB=2米时涵洞的顶点与水面的距离为4米,这时离开水面2米处涵洞宽DE是多少?
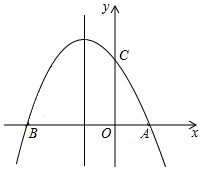 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴相交于点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴相交于点B. 如图所示,点D,E分别在边AC,AB上,且AD•AC=AE•AB,已知BD⊥AC,求证:CE⊥AB.
如图所示,点D,E分别在边AC,AB上,且AD•AC=AE•AB,已知BD⊥AC,求证:CE⊥AB.