题目内容
1.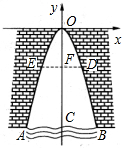 某涵洞的截面边缘成抛物线形,现测得当水面宽AB=2米时涵洞的顶点与水面的距离为4米,这时离开水面2米处涵洞宽DE是多少?
某涵洞的截面边缘成抛物线形,现测得当水面宽AB=2米时涵洞的顶点与水面的距离为4米,这时离开水面2米处涵洞宽DE是多少?
分析 根据点B的坐标利用待定系数法求得函数解析式,再求出离开水面2米处即y=-2时x的值,从而得出答案.
解答 解:根据题意知点B坐标为(1,-4),
设抛物线解析式为y=ax2,
将点B(1,-4)代入,得:a=-4,
∴抛物线解析式为y=-4x2,
当y=-2时,由-4x2=-2得x=±$\frac{\sqrt{2}}{2}$,
∴DE=$\frac{\sqrt{2}}{2}$-(-$\frac{\sqrt{2}}{2}$)=$\sqrt{2}$,
答:这时离开水面2米处涵洞宽DE是$\sqrt{2}$米.
点评 本题主要考查了用待定系数法求二次函数的解析式及二次函数的实际应用,根据图中信息得出函数经过的点的坐标是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
11.下列图案中,是中心对称图形的有( )
| A. |  | B. |  | C. |  | D. |  |
12.互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为720元,按标价的五折销售,仍可获利20%,则这件商品的进价为( )
| A. | 200元 | B. | 144元 | C. | 300元 | D. | 360元 |
16.如果把分式$\frac{x-y}{x+y}$中的和都扩大了3倍,那么分式的值( )
| A. | 扩大3倍 | B. | 缩小6倍 | C. | 缩小3倍 | D. | 不变 |
13.下列函数中,y是x的二次函数的是( )
| A. | y=2x-1 | B. | y=-$\frac{1}{x}$ | C. | y=x-x2 | D. | y=$\frac{1}{{x}^{2}}$+x |
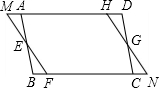 如图四边形ABCD、MFNH都是平行四边形,MAHD和BFCN都在一直线上,HD=FB.
如图四边形ABCD、MFNH都是平行四边形,MAHD和BFCN都在一直线上,HD=FB.