题目内容
 已知在平面直角坐标系中四边形A1B1C1D1,其中A1(2,-2)、
已知在平面直角坐标系中四边形A1B1C1D1,其中A1(2,-2)、B1(0,2)、C1(-2,1)、D1(0,-1),A1B1、C1D1分别与x轴交于点P(1,0)和Q(-1,0).
(1)画出四边形A1B1C1D1关于y轴对称的四边形A2B2C2D2,并写出各顶点坐标;
(2)求四边形A1B1C1D1与A2B2C2D2重叠部分的面积;
(3)在坐标系里适当地选取一点E,写出它的坐标,使得△B1OP与△B1EC1全等,并能以此证明A1B1⊥C1B1(写出简要的证明过程).
考点:作图-轴对称变换,全等三角形的判定
专题:作图题
分析:(1)根据网格结构找出点A2、B2、C2、D2的位置,然后顺次连接即可,再根据平面直角坐标系写出各点的坐标即可;
(2)根据轴对称性,重叠部分的面积等于2S△B1PD1列式计算即可得解;
(3)取E(-2,2),根据点的坐标可得OP=EC1,OB1=EB1,然后利用“边角边”证明△B1OP与△B1EC1全等,再根据全等三角形对应角相等可得∠OB1P=∠EB1C1,然后求出∠C1B1A1=90°,根据垂直的定义证明即可.
(2)根据轴对称性,重叠部分的面积等于2S△B1PD1列式计算即可得解;
(3)取E(-2,2),根据点的坐标可得OP=EC1,OB1=EB1,然后利用“边角边”证明△B1OP与△B1EC1全等,再根据全等三角形对应角相等可得∠OB1P=∠EB1C1,然后求出∠C1B1A1=90°,根据垂直的定义证明即可.
解答: 解:(1)四边形A2B2C2D2如图所示,A2(-2,-2),B2(0,2),C2(2,1),D2(0,-1);
解:(1)四边形A2B2C2D2如图所示,A2(-2,-2),B2(0,2),C2(2,1),D2(0,-1);
(2)重叠部分为四边形D1PB1Q,
由对称性知,重叠部分的面积=2S△B1PD1,
所以,重叠部分的面积=2×
×3×2=6;
(3)取E(-2,2),连接EB1、EC1,
在△B1OP与△B1EC1中,
,
∴△B1OP≌△B1EC1(SAS),
∴∠OB1P=∠EB1C1,
∴∠C1B1A1=∠C1B1O+∠OB1P=∠C1B1O+∠EB1C1=∠EB1O=90°,
∴A1B1⊥C1B1.
[注:选取(0,1)也可].
 解:(1)四边形A2B2C2D2如图所示,A2(-2,-2),B2(0,2),C2(2,1),D2(0,-1);
解:(1)四边形A2B2C2D2如图所示,A2(-2,-2),B2(0,2),C2(2,1),D2(0,-1);(2)重叠部分为四边形D1PB1Q,
由对称性知,重叠部分的面积=2S△B1PD1,
所以,重叠部分的面积=2×
| 1 |
| 2 |
(3)取E(-2,2),连接EB1、EC1,
在△B1OP与△B1EC1中,
|
∴△B1OP≌△B1EC1(SAS),
∴∠OB1P=∠EB1C1,
∴∠C1B1A1=∠C1B1O+∠OB1P=∠C1B1O+∠EB1C1=∠EB1O=90°,
∴A1B1⊥C1B1.
[注:选取(0,1)也可].
点评:本题考查了利用轴对称变换作图,全等三角形的判定与性质,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
相关题目
若x+m与x+
乘积的值不含x项,则m的值为( )
| 1 |
| 4 |
A、
| ||
| B、4 | ||
C、-
| ||
| D、-4 |
 如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P.已知正方形ABCD的三个顶点为A(4,4),B(6,4),D(4,6).
如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P.已知正方形ABCD的三个顶点为A(4,4),B(6,4),D(4,6).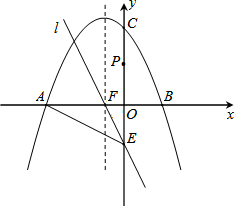 如图,抛物线C1:y=ax2+bx+4的图象与两坐标轴分别交于A、B、C三点,经过点E(0,-2)的直线l:y=kx-2(k≠0)与x轴、抛物线的对称轴x=-1交于点F.
如图,抛物线C1:y=ax2+bx+4的图象与两坐标轴分别交于A、B、C三点,经过点E(0,-2)的直线l:y=kx-2(k≠0)与x轴、抛物线的对称轴x=-1交于点F.