题目内容
 如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P.已知正方形ABCD的三个顶点为A(4,4),B(6,4),D(4,6).
如图,在直角坐标系中,点P的坐标是(n,0)(n>0),抛物线y=-x2+bx+c经过原点O和点P.已知正方形ABCD的三个顶点为A(4,4),B(6,4),D(4,6).(1)请用含有n的代数式表示抛物线的解析式为y=
(2)若直线AD与抛物线交于点N,与x轴交于点M,tan∠NOP=2,当点Q(m,2m-5)在第一象限的抛物线上时,求Q点及其关于直线MN对称点Q′的坐标;
(3)若抛物线经过正方形区域ABCD(含边界),请直接写出n的取值范围.
考点:二次函数综合题
专题:
分析:(1)应用待定系数法即可求得.
(2)根据tan∠NOP=
=2求得N(4,8),进而求得抛物线的解析式,根据Q(m,2m-5)在抛物线上,可求得m的值,从而求得Q的坐标,即可求得关于直线MN对称点Q′的坐标.
(3)将A(4,4),C(6,6)分别代入y=-x2+nx;即可求得.
(2)根据tan∠NOP=
| NM |
| OM |
(3)将A(4,4),C(6,6)分别代入y=-x2+nx;即可求得.
解答:解:(1)∵抛物线y=-x2+bx+c经过原点O和点P(n,0).
∴
解得
∴y=-x2+nx;
(2)∵在Rt△OMN中tan∠NOP=2,而tan∠NOP=
,
∵AD⊥x轴,A(4,4),D(4,6),
∴OM=4,MN=8,N(4,8),
∴将点N的坐标代入y=-x2+nx,得n=6,
即y=-x2+6x,
∵Q(m,2m-5)在抛物线上,
∴2m-5=-m2+6m,
即m2-4m-5=0,
∴m=5或m=-1,
∵点Q在第一象限,
∴Q(5,5),
∵直线MN为x=4,
∴点Q关于直线MN对称的点的坐标为Q′(3,5);
(3)5≤n≤7.
∵把A(4,4)代入y=-x2+nx得:4=-16+4n,解得:n=5,
把C(6,6)代入y=-x2+nx得:6=-36+6n,解得:n=7,
∴5≤n≤7.
∴
|
|
∴y=-x2+nx;
(2)∵在Rt△OMN中tan∠NOP=2,而tan∠NOP=
| NM |
| OM |
∵AD⊥x轴,A(4,4),D(4,6),
∴OM=4,MN=8,N(4,8),
∴将点N的坐标代入y=-x2+nx,得n=6,
即y=-x2+6x,
∵Q(m,2m-5)在抛物线上,
∴2m-5=-m2+6m,
即m2-4m-5=0,
∴m=5或m=-1,
∵点Q在第一象限,
∴Q(5,5),
∵直线MN为x=4,
∴点Q关于直线MN对称的点的坐标为Q′(3,5);
(3)5≤n≤7.
∵把A(4,4)代入y=-x2+nx得:4=-16+4n,解得:n=5,
把C(6,6)代入y=-x2+nx得:6=-36+6n,解得:n=7,
∴5≤n≤7.
点评:本题考查了待定系数法求解析式,三角函数的应用,关于直线对称的性质以及解不等式的知识等.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
下列各因式分解正确的是( )
| A、a2+ab-b2=(a+b)(a-b)+ab | ||
| B、(x+5)(x-5)=x2-25 | ||
C、2x2+4x+5=2x(x+2+
| ||
| D、m2-6mn+9n2=(m-3n)2 |
无论a为何值,直线y=x+2a与y=-x+4的交点不可能在第( )象限.
| A、1 | B、2 | C、3 | D、4 |
 已知在平面直角坐标系中四边形A1B1C1D1,其中A1(2,-2)、
已知在平面直角坐标系中四边形A1B1C1D1,其中A1(2,-2)、 已知,如图△ABC中,AB=26,BC=20,BC边上的中线AD=24,
已知,如图△ABC中,AB=26,BC=20,BC边上的中线AD=24,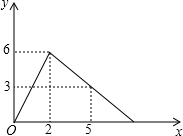 某医院研究所研发了一种新药,在临床试验时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(小时)的变化情况如图所示.?
某医院研究所研发了一种新药,在临床试验时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(小时)的变化情况如图所示.?