题目内容
已知：等腰三角形两边长分别为9cm，5cm，则周长是（ ）
| A、19cm |
| B、23cm |
| C、19cm或23cm |
| D、不能确定 |
考点：等腰三角形的性质,三角形三边关系
专题：分类讨论
分析：分9cm是腰长与底边长两种情况，再结合三角形的三边关系讨论求解．
解答：解：①若9cm是腰长，则三角形的三边分别为9cm、9cm、5cm，
能组成三角形，
周长=9+9+5=23cm，
②若9cm是底边长，则三角形的三边分别为9cm、5cm、5cm，
能组成三角形，
周长=9+5+5=19cm，
综上所述，三角形的周长为23cm或19cm．
故选C．
能组成三角形，
周长=9+9+5=23cm，
②若9cm是底边长，则三角形的三边分别为9cm、5cm、5cm，
能组成三角形，
周长=9+5+5=19cm，
综上所述，三角形的周长为23cm或19cm．
故选C．
点评：本题考查了等腰三角形的性质，三角形的三边关系，难点在于分情况讨论并利用三角形三边关系判断是否能组成三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在雨地里放置一个无盖的容器，如果雨水均匀地落入容器，容器水面高度h与时间t的函数图象如图所示，那么这个容器的形状可能是（ ）
如图，在平面直角坐标系中，△ABC的三个顶点A（4，3），B（1，4），C（2，1）．已知三条线段长分别为a、b、c，a＜b＜c（a、b、c均为整数），若c=6，则线段a、b、c能组成三角形的情形有（ ）
| A、3种 | B、4种 | C、5种 | D、6种 |
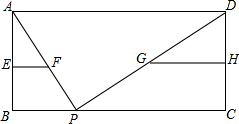如图，已知平行四边形ABCD中，AD=10cm，点P在边BC边上移动，点E、F、G、H分别是AB、AP、DP、DC的中点，请探索在移动过程中，EF+GH的值是否改变？若不变，请求EF+GH的值．
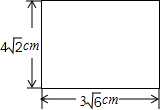如图，已知一块矩形木板的长和宽分别为3