题目内容
用2个全等的如图(1)所示的直角三角形拼成一个如图(2)所示的直角梯形,你能利用图形的面积之间的关系说明勾股定理吗?
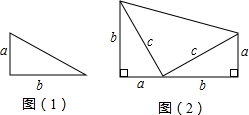

考点:勾股定理的证明
专题:
分析:用三角形的面积和、梯形的面积来表示这个图形的面积,从而列出等式,发现边与边之间的关系.
解答:证明:此图可以这样理解,有三个直角三角形,其面积分别为
ab,
ab和
c2.
还有一个直角梯形,其面积为
(a+b)(a+b).
由图形可知:
(a+b)(a+b)=
ab+
ab+
c2
整理得(a+b)2=2ab+c2,a2+b2+2ab=2ab+c2,
则a2+b2=c2.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
还有一个直角梯形,其面积为
| 1 |
| 2 |
由图形可知:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得(a+b)2=2ab+c2,a2+b2+2ab=2ab+c2,
则a2+b2=c2.
点评:此题主要考查了勾股定理的证明,解题时利用了三角形的面积公式:底×高÷2,和梯形的面积公式:(上底+下底)×高÷2.

练习册系列答案
相关题目
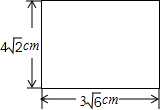 如图,已知一块矩形木板的长和宽分别为3
如图,已知一块矩形木板的长和宽分别为3| 6 |
| 2 |
现有若干个三角形,在所有的内角中,有4个直角,5个钝角,27个锐角,则在这些三角形中锐角三角形的个数是( )
| A、3 | B、4或5 | C、6或7 | D、8 |
 如图,AE是位于公路边的电线杆,高为12m,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根为6m的水泥撑杆BD,用于撑起电线.已知两根杆子之间的距离为8m,电线CD与水平线AC的夹角为60°.求电线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计).
如图,AE是位于公路边的电线杆,高为12m,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根为6m的水泥撑杆BD,用于撑起电线.已知两根杆子之间的距离为8m,电线CD与水平线AC的夹角为60°.求电线CDE的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大小忽略不计). 如图,在平面直角坐标系中,△ABC的三个顶点A(4,3),B(1,4),C(2,1).
如图,在平面直角坐标系中,△ABC的三个顶点A(4,3),B(1,4),C(2,1).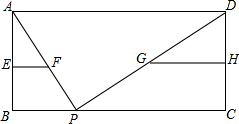 如图,已知平行四边形ABCD中,AD=10cm,点P在边BC边上移动,点E、F、G、H分别是AB、AP、DP、DC的中点,请探索在移动过程中,EF+GH的值是否改变?若不变,请求EF+GH的值.
如图,已知平行四边形ABCD中,AD=10cm,点P在边BC边上移动,点E、F、G、H分别是AB、AP、DP、DC的中点,请探索在移动过程中,EF+GH的值是否改变?若不变,请求EF+GH的值.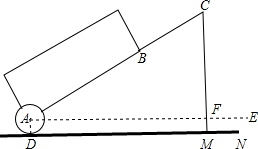
 如图,△ABC中,AB的中垂线DE交AB于E,交BC于D,若CB=10,AC=6,则△ACD的周长为
如图,△ABC中,AB的中垂线DE交AB于E,交BC于D,若CB=10,AC=6,则△ACD的周长为