题目内容
20．
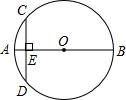如图，AB是⊙O的直径，弦CD⊥AB于点E，已知，CD=8，AE=2，则⊙O的半径长是（ ）| A． | 10 | B． | 6 | C． | 5 | D． | 3 |
分析 连接OC，根据垂径定理求出CE，根据勾股定理得出方程，求出方程的解即可．
解答 解：设半径为R，
连接OC，
∵AB是⊙O的直径，弦CD⊥AB于点E，CD=8，
∴∠CEO=90°，CE=DE=4，
由勾股定理得：OC2=CE2+OE2，
R2=42+（R-2）2，
解得：R=5，
则⊙O的半径长是5，
故选C．
点评 本题考查了垂径定理和勾股定理的应用，能求出CE=DE是解此题的关键，注意：垂直于弦的直径平分弦．
练习册系列答案
相关题目
如图，AB是⊙O的弦，AB=7$\sqrt{2}$，点C是⊙O上的一动点，且∠ACB=45°．若点M，N分别是AB，BC的中点，则MN长的最大值是7．
8．
如图CA=CD，CB=CE，欲证△ABC≌△DEC，可补充条件（ ）
如图CA=CD，CB=CE，欲证△ABC≌△DEC，可补充条件（ ）| A． | ∠BCE=∠ACD | B． | ∠B=∠E | C． | ∠A=∠D | D． | ∠BCA=∠ACD |
15．与$\sqrt{3}$是同类二次根式的是（ ）
| A． | $\sqrt{\frac{1}{3}}$ | B． | $\sqrt{9}$ | C． | $\sqrt{18}$ | D． | $\sqrt{2}$ |
12．在下列语句中表述正确的是（ ）
| A． | 延长直线AB | B． | 延长射线AB | C． | 作直线AB=BC | D． | 延长线段AB到C |
9．下列几组数中不能作为直角三角形三边长度的是（ ）
| A． | a=7，b=24，c=25 | B． | a=1.5，b=2，c=2.5 | C． | a=$\frac{1}{3}$，b=$\frac{1}{4}$，c=$\frac{1}{5}$ | D． | a=15，b=8，c=17 |
如图，已知抛物线y=x2+bx+c的对称轴为x=2，点A，B均在抛物线上，且AB与x轴平行，其中点A的坐标为（0，3），则点B的坐标为（4，3）．