题目内容
11. 如图,AB是⊙O的弦,AB=7$\sqrt{2}$,点C是⊙O上的一动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是7.
如图,AB是⊙O的弦,AB=7$\sqrt{2}$,点C是⊙O上的一动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是7.
分析 根据中位线定理得到MN的最大时,AC最大,当AC最大时是直径,从而求得直径后就可以求得最大值.
解答 解:∵点M,N分别是AB,BC的中点,
∴MN=$\frac{1}{2}$AC,
∴当AC取得最大值时,MN就取得最大值,
当AC时直径时,最大,如图所示, ∵∠ACB=∠D=45°,AB=7$\sqrt{2}$,∠ABD=90°,
∵∠ACB=∠D=45°,AB=7$\sqrt{2}$,∠ABD=90°,
∴AD=$\sqrt{2}$AB=14,
∴MN=$\frac{1}{2}$AD=7,
故答案为:7.
点评 本题考查了三角形的中位线定理、等腰直角三角形的性质及圆周角定理,解题的关键是了解当什么时候MN的值最大,难度不大.

练习册系列答案
相关题目
1.已知抛物线y=-x2+6x-5,它的顶点坐标为( )
| A. | (-3,4) | B. | (3,-4) | C. | (-3,-4) | D. | (3,4) |
6.抛物线y=ax2+bx+c上部分点的横坐标x纵坐标y的对应值如下表,则下列说法中正确的有②③④.(填序号)
①当x>1时,y随x的增大而增大 ②抛物线的对称轴为直线x=$\frac{1}{2}$.
③当x=2时,y=-1 ④方程ax2+bx+c=0一个负数解x1满足-1<x1<0.
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -37 | -21 | -9 | -1 | 3 | 3 | … |
③当x=2时,y=-1 ④方程ax2+bx+c=0一个负数解x1满足-1<x1<0.
3.计算(-1)2-(-2)的结果是( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
20.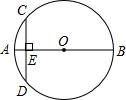 如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )| A. | 10 | B. | 6 | C. | 5 | D. | 3 |
1.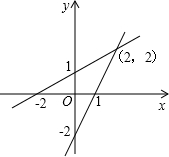 如图,直线l1、l2的交点坐标可以看作方程组( )的解.
如图,直线l1、l2的交点坐标可以看作方程组( )的解.
 如图,直线l1、l2的交点坐标可以看作方程组( )的解.
如图,直线l1、l2的交点坐标可以看作方程组( )的解.| A. | $\left\{\begin{array}{l}{x-2y=-2}\\{2x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y=-x+1}\\{y=2x-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x-2y=-1}\\{2x-y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=2x+1}\\{y=2x-2}\end{array}\right.$ |

 如图,OA是⊙O的直径,OA=6,CD是圆B的切线,D为切点∠DOC=30°,则点C的坐标为(9,0).
如图,OA是⊙O的直径,OA=6,CD是圆B的切线,D为切点∠DOC=30°,则点C的坐标为(9,0).