题目内容
10.关于x的方程-x2-2x+2-t=0在-3≤x<2上有两个不同的实数根,则t的取值范围为-1≤t<3.分析 令y=-x2-2x+2-t,根据方程-x2-2x+2-t=0解的情况即可得出抛物线与x轴交点横坐标的范围,进而可得出关于t的一元一次不等式组,解不等式组即可得出结论.
解答 解:令y=-x2-2x+2-t,则二次函数的对称轴为x=-$\frac{-2}{2×(-1)}$=-1.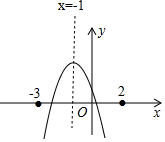
∵关于x的方程-x2-2x+2-t=0在-3≤x<2上有两个不同的实数根,
∴$\left\{\begin{array}{l}{-(-1)^{2}-2×(-1)+2-t>0}\\{-(-3)^{2}-2×(-3)+2-t≤0}\\{-{2}^{2}-2×2+2-t≤0}\end{array}\right.$,
解得:-1≤t<3.
故答案为:-1≤t<3.
点评 本题考查了抛物线与x轴的交点,根据抛物线与x轴交点横坐标的范围找出关于t的一元一次不等式组是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
1.已知抛物线y=-x2+6x-5,它的顶点坐标为( )
| A. | (-3,4) | B. | (3,-4) | C. | (-3,-4) | D. | (3,4) |
18.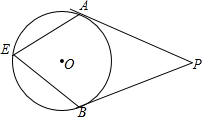 如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=50°,则∠P为( )
如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=50°,则∠P为( )
 如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=50°,则∠P为( )
如图,PA,PB分别是⊙O的切线,A,B分别为切点,点E是⊙O上一点,且∠AEB=50°,则∠P为( )| A. | 130° | B. | 80° | C. | 50° | D. | 45° |
5.圆的直径为5cm,如果点P到圆心O的距离是d,则( )
| A. | 当d=4 cm时,点P在⊙O内 | B. | 当d=5 cm时,点P在⊙O上 | ||
| C. | 当d=2.5 cm时,点P在⊙O上 | D. | 当d=3 cm时,点P在⊙O内 |
20.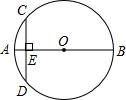 如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )| A. | 10 | B. | 6 | C. | 5 | D. | 3 |
