题目内容
9.下列几组数中不能作为直角三角形三边长度的是( )| A. | a=7,b=24,c=25 | B. | a=1.5,b=2,c=2.5 | C. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ | D. | a=15,b=8,c=17 |
分析 利用勾股定理的逆定理:如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.最长边所对的角为直角.由此判定即可.
解答 A、∵72+242=252,∴三条线段能组成直角三角形,故A选项错误;
B、∵1.52+22=2.522+4=6,∴能组成直角三角形,故B选项错误;
C、∵($\frac{1}{4}$)2+($\frac{1}{5}$)2≠($\frac{1}{3}$)2,∴三条线段不能组成直角三角形,故C选项正确;
D、∵152+82=172,∴三条线段能组成直角三角形,故D选项错误;
故选:C.
点评 此题考查了勾股定理逆定理的运用,判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可,注意数据的计算.

练习册系列答案
相关题目
20.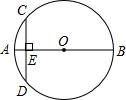 如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,已知,CD=8,AE=2,则⊙O的半径长是( )| A. | 10 | B. | 6 | C. | 5 | D. | 3 |
14.设三角形的三边长分别等于下列各组数,能构成直角三角形的是( )
| A. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | $\frac{1}{6}$,$\frac{1}{8}$,$\frac{1}{10}$ | D. | 4,5,6 |
1.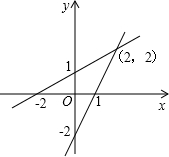 如图,直线l1、l2的交点坐标可以看作方程组( )的解.
如图,直线l1、l2的交点坐标可以看作方程组( )的解.
 如图,直线l1、l2的交点坐标可以看作方程组( )的解.
如图,直线l1、l2的交点坐标可以看作方程组( )的解.| A. | $\left\{\begin{array}{l}{x-2y=-2}\\{2x-y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y=-x+1}\\{y=2x-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x-2y=-1}\\{2x-y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=2x+1}\\{y=2x-2}\end{array}\right.$ |
18.调查八年级某班50名学生一周做家务所用时间,得到下表中数据:这组数据的中位数是2.4.
| 每周做家务的时间(小时) | 0 | 1 | 1.2 | 2 | 2.4 | 3 | 3.5 | 4 | 合计 |
| 人数 | 2 | 2 | 6 | 12 | 13 | 4 | 3 | 50 |

 如图,D是线段AB中点,E是线段BC中点,若AC=10,则线段DE=5.
如图,D是线段AB中点,E是线段BC中点,若AC=10,则线段DE=5.