题目内容
7. 如图,D、E分别是△ABC的边AB、AC上的中点,则S△ADE:SDECB=1:3.
如图,D、E分别是△ABC的边AB、AC上的中点,则S△ADE:SDECB=1:3.
分析 根据三角形中位线定理可知△ADE∽△ABC相似且相似比是1:2,根据相似三角形的性质可以求得△ADE与△ABC的面积之比,则易求S△ADE:SDECB.
解答 解:如图,∵D、E分别是AB、AC的中点,
∴DE∥BC,且EDE=$\frac{1}{2}$BC,
∴△ADE∽△ABC,
∴DE:BC=1:2,
∴△ADE与△ABC的面积之比为1:4,
∴△ADE与四边形BCED的面积之比是1:3.
故答案为1:3.
点评 本题考查了三角形的中位线的性质:三角形的中位线等于第三边的一半.同时考查对相似三角形性质的理解,相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目
 印度数学家什迦罗(1141年-1225年)曾提出过“荷花问题”:
印度数学家什迦罗(1141年-1225年)曾提出过“荷花问题”: 如图,在Rt△ABC中,∠BAC=90°,AB=AC=$\sqrt{2}$,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1,矩形PDFE的面积为S2,运y=S1+S2,则y与x的关系式是y=$-{x}^{2}+\frac{3}{2}x$.
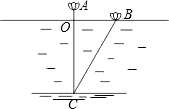
如图,在Rt△ABC中,∠BAC=90°,AB=AC=$\sqrt{2}$,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1,矩形PDFE的面积为S2,运y=S1+S2,则y与x的关系式是y=$-{x}^{2}+\frac{3}{2}x$. 如图,在正方形网格中,每个小正方形的边长均相等,点A、B、O均在格点处,则cos∠AOB=$\frac{3}{5}$.
如图,在正方形网格中,每个小正方形的边长均相等,点A、B、O均在格点处,则cos∠AOB=$\frac{3}{5}$.