题目内容
下列说法正确的是 ( )
A. 两个全等的图形可看做其中一个是由另一个平移得到的
B. 由平移得到的两个图形对应点连线互相平行(或共线)
C. 由平移得到的两个等腰三角形周长一定相等，但面积未必相等
D. 边长相等的两个正方形一定可以通过平移得到
B
【解析】试题分析：A、全等三角形仅仅是反映了两个三角形的形状和大小关系，而平移既需要两个三角形全等，还需要两个三角形有一种特殊的位置关系，故错误；
B、符合平移的性质，故正确；
C、由平移得到的两个等腰三角形全等，面积必相等，故错误；
D、平移还需要具备一种特殊的位置关系，故错误．
故选B．
如图所示，△ABC是不等边三角形，DE=BC，以D、E为两个顶点作位置不同的三角形，使所作三角形与△ABC全等，这样的三角形最多可以画出（ ）个．
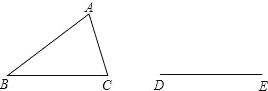
A．2 B．4 C．6 D．8
B.
【解析】
试题分析：可以做4个，分别是以D为圆心，AB为半径，作圆，以E为圆心，AC为半径，作圆．两圆相交于两点（D，E上下各一个），经过连接后可得到两个．然后以D为圆心，AC为半径，作圆，以E为圆心，AB为半径，作圆．两圆相交于两点（D，E上下各一个），经过连接后可得到两个．如图.
故选：B. 在Rt△ABC中，∠C＝90°，AC＝2，BC＝3，那么下列各式中，正确的是( )
A. sin B＝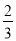
B. cos B＝
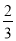C. tan B＝
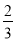D. tan B＝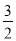
C
【解析】∵∠C＝90°，AC＝2，BC＝3，∴AB= ，
∴sinB= ，cosB=，tanB=，
故选C. 菱形以特殊的对称美而深受人们的喜爱，在生产生活中有着广泛的应用，小龙家里有一面长4.2m、宽2.8m的墙壁准备装修，现有如图甲所示的型号瓷砖，其形状是一块长30cm、宽20cm的矩形，中间白色部分为菱形，阴影部分为带淡蓝色花纹的全等的四个直角三角形，解答下列各问：
（1）小龙家里的墙壁最少要贴这种瓷砖多少块？
（2）全部贴满后，这面墙壁上有多少个有淡蓝色花纹的菱形？
(1)196;(2)169
【解析】试题分析：（1）根据墙壁的长与宽以及矩形瓷砖的长与宽进行计算求出所需要贴的瓷砖的行数与列数，然后进行计算即可得解；
（2）根据（1）中结论即可求出淡蓝色花纹的菱形个数．
试题解析：
【解析】
（1）4.2m＝420cm，2.8m＝280cm，
∵420÷30＝14，280÷20＝14，
∴贴满墙壁需要14行14列瓷砖，
... 下列现象：(1)电风扇的转动；(2)打气筒打气时，活塞的运动；(3)钟摆的摆动；(4)传送带上瓶装饮料的移动．其中属于平移的是_________．
(2)(4)
【解析】试题分析：（1）电风扇的转动是旋转，不属于平移；
（2）打气筒打气时，活塞的运动属于平移；
（3）钟摆的摆动是旋转，不属于平移；
（4）传送带上瓶装饮料的移动符合平移的性质，属于平移．
故选D． 如图，已知∠A=∠D=90°，E、F在线段BC上，DE与AF交于点O，且AB=CD，BE=CF．求证：Rt△ABF≌Rt△DCE．
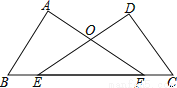
证明见解析.
【解析】由于△ABF与△DCE是直角三角形，根据直角三角形全等的判定的方法即可证明．
证明：∵BE=CF，
∴BE+EF=CF+EF，即BF=CE，
∵∠A=∠D=90°，
∴△ABF与△DCE都为直角三角形，
在Rt△ABF和Rt△DCE中，
BC=CE，AB=CD，
∴Rt△ABF≌Rt△DCE（HL）． 已知，如图，△ABC中，∠BAC=90°，AD⊥BC于D，则图中相等的锐角的对数有（ ）
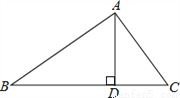
A. 4对 B. 3对 C. 2对 D. 1对
C
【解析】【解析】
相等的锐角有：∠B=∠CAD，∠C=∠BAD共2对．故选C． 文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时，画出图形，写出“已知”，“求证”（如图），她们对各自所作的辅助线描述如下：
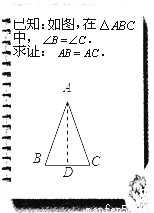
文文：“过点A作BC的中垂线AD，垂足为D”；
彬彬：“作△ABC的角平分线AD”．
数学老师看了两位同学的辅助线作法后，说：“彬彬的作法是正确的，而文文的作法需要订正．”
（1）请你简要说明文文的辅助线作法错在哪里；
（2）根据彬彬的辅助线作法，完成证明过程．
（1）作辅助线不能同时满足两个条件；（2）证明见解析.
【解析】试题分析：（1）线段BC的中垂线可以直接作出的，不需要附带“过点A作”；
（2）根据已知条件利用AAS可证△ABD≌△ACD，得出AB=AC．
试题解析：（1）作辅助线不能同时满足两个条件；
（2）证明：作△ABC的角平分线AD．
∴∠BAD=∠CAD，
在△ABD与△ACD中，
∴△ABD≌... 写出一个解集为x＞1的一元一次不等式：__________．
2x-1＞1（答案不唯一）
【解析】试题分析：【解析】
移项，得x﹣1＞0（答案不唯一）．
故答案为x﹣1＞0．