题目内容
20.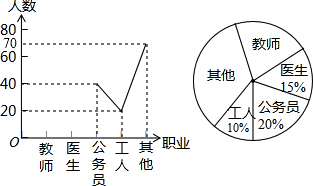 某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )| A. | 被调查的学生有200人 | |
| B. | 扇形图中公务员部分所对应的圆心角为72° | |
| C. | 若全校有2000名学生则喜欢教师职业的大约有400人 | |
| D. | 被调查的学生中喜欢其它职业的占40% |
分析 用工人的人数除以它所占的百分比得到样本容量,则可对A进行判断;用360°乘以公务员所占的百分比得到扇形图中公务员部分所对应的圆心角,则可对B进行判断;先计算出其他职业所占的百分比,再计算出教师职业所占的百分比,然后利用样本估计总体,用2000乘以样本中教师职业所占的百分比可估计出全校学生喜欢教师职业的人数,于是可对C、D进行判断.
解答 解:A、20÷10%=200,则被调查的总人数为200人,所以A选项的说法正确;
B、扇形图中公务员部分所对应的圆心角=360°×20%=72°,所以B选项的说法正确;
C、其他职业所占的百分比=$\frac{70}{200}$×100%=35%,则教师职业所占的百分比=1-10%-20%-15%-35%=20%,2000×20%=400,估计全校有2000名学生则喜欢教师职业的大约有400人,所以C选项的说法正确;
D、被调查的学生中喜欢其它职业的占35%,所以D选项的说法错误.
故选D.
点评 本题考查了折线统计图:折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.也考查了扇形统计图和用样本估计总体.

练习册系列答案
相关题目
11. 如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,OC=5,则OD的长为( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,OC=5,则OD的长为( )
 如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,OC=5,则OD的长为( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,且AB=8,OC=5,则OD的长为( )| A. | 1 | B. | 2 | C. | 2.5 | D. | 3 |
8. 如图,AB∥CD,若∠B=70°,则∠E+∠F等于( )
如图,AB∥CD,若∠B=70°,则∠E+∠F等于( )
 如图,AB∥CD,若∠B=70°,则∠E+∠F等于( )
如图,AB∥CD,若∠B=70°,则∠E+∠F等于( )| A. | 20° | B. | 70° | C. | 100° | D. | 110° |
12. 如图,点D、E分别是△ABC的边AB边和AC边上的点,且DE∥BC,∠AED=64°,EC是∠DEB的角平分线,则∠ECB的度数为( )
如图,点D、E分别是△ABC的边AB边和AC边上的点,且DE∥BC,∠AED=64°,EC是∠DEB的角平分线,则∠ECB的度数为( )
 如图,点D、E分别是△ABC的边AB边和AC边上的点,且DE∥BC,∠AED=64°,EC是∠DEB的角平分线,则∠ECB的度数为( )
如图,点D、E分别是△ABC的边AB边和AC边上的点,且DE∥BC,∠AED=64°,EC是∠DEB的角平分线,则∠ECB的度数为( )| A. | 78° | B. | 68° | C. | 58° | D. | 48° |
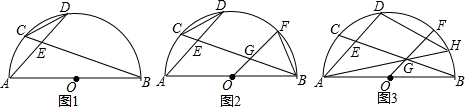
 如图,己知抛物线y=ax2+bx-2与y轴交于点C,与x轴交于A,B两点,在△ABC中,tan∠OAC=2,S△ABC=4,
如图,己知抛物线y=ax2+bx-2与y轴交于点C,与x轴交于A,B两点,在△ABC中,tan∠OAC=2,S△ABC=4,