题目内容
10.甲、乙两个不透明的口袋,甲口袋中装有3个分别标有数字1,2,3的小球,乙口袋中装有2个分别标有数字4,5的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字,再从乙口袋中摸出一个小球记下数字.(1)请用列表或树状图的方法(只选其中一种),表示出两次所得数字可能出现的所有结果;
(2)求出两个数字之和能被3整除的概率.
分析 先根据题意画树状图,再根据所得结果计算两个数字之和能被3整除的概率.
解答 解:(1)树状图如下:
(2)∵共6种情况,两个数字之和能被3整除的情况数有2种,
∴两个数字之和能被3整除的概率为$\frac{2}{6}$,
即P(两个数字之和能被3整除)=$\frac{1}{3}$.
点评 本题主要考查了列表法与树状图法,解决问题的关键是掌握概率的计算公式.随机事件A的概率P(A)等于事件A可能出现的结果数除以所有可能出现的结果数.

练习册系列答案
相关题目
20.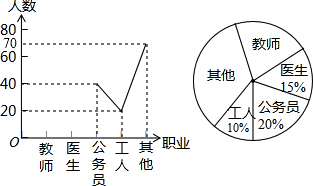 某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
 某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )| A. | 被调查的学生有200人 | |
| B. | 扇形图中公务员部分所对应的圆心角为72° | |
| C. | 若全校有2000名学生则喜欢教师职业的大约有400人 | |
| D. | 被调查的学生中喜欢其它职业的占40% |
2.在一个有12万人的小镇,随机调查了3000人,其中500人看某电视台的早间新闻.那么,在该小镇随便问一个人,他看该电视台早间新闻的概率大约是( )
| A. | $\frac{1}{240}$ | B. | $\frac{1}{40}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |




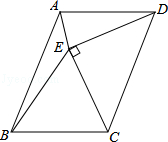 如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是135°.
如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是135°.