题目内容
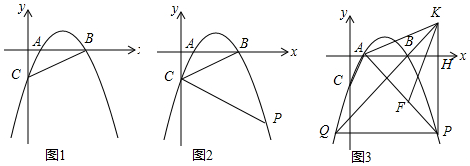
15. 如图,己知抛物线y=ax2+bx-2与y轴交于点C,与x轴交于A,B两点,在△ABC中,tan∠OAC=2,S△ABC=4,
如图,己知抛物线y=ax2+bx-2与y轴交于点C,与x轴交于A,B两点,在△ABC中,tan∠OAC=2,S△ABC=4,(1)求点A,B,C的坐标;
(2)求抛物线的解析式;
(3)设点E在x轴上,点F在抛物线上,如果A,C,E,F四点构成平行四边形,请直接写出点E的坐标(不必书写计算过程)
分析 (1)先求出C点坐标得到OC=2,再在Rt△OAC中利用正切定义求出OA,从而得到A点坐标,然后利用三角形面积公式求出AB,从而得到B点坐标;
(2)设交点式y=a(x+1)(x-3),然后把C点坐标代入求出a即可;
(3)如图,先确定抛物线的对称轴为直线x=1,分类讨论:当AC为对角线,利用AE1∥CF1得到F1(2,-2),则有AE1=CF1=2,于是可得到E1点坐标;当AC为边,平行四边形为ACFE时,利用AE2∥CF2同样可得AE2=CF2=2,易得E2点的坐标;当AC为边,平行四边形为ACEF时,利用平行四边形的性质可判断点F和点C到x轴的距离相等,则点F的纵坐标为2,再计算函数值为2所对应的自变量的值得到F3(1-$\sqrt{7}$,2),F4(1+$\sqrt{7}$,0),然后利用平移和确定点E3和点E4的坐标.
解答 解:(1)当y=0时,y=ax2+bx-2=-2,则C(0,-2),
在Rt△OAC中,∵tan∠OAC=$\frac{OC}{OA}$,
∴OA=$\frac{OC}{2}$=1,
∴A(-1,0);
∵S△ABC=4,
∴$\frac{1}{2}$•AB•2=4,解得AB=4,
∴OB=3,
∴B(3,0);
(2)设抛物线解析式为y=a(x+1)(x-3),
把C(0,-2)代入得a•1•(-3)=-2,
解得a=$\frac{2}{3}$,
∴抛物线解析式为y=$\frac{2}{3}$x2-$\frac{4}{3}$x-2;
(3)如图,抛物线的对称轴为直线x=1,
当AC为对角线,∵AE1∥CF1,即CF1平行x轴,
∴点C和点F1关于直线x=1对称,
∴F1(2,-2),
∴AE1=CF1=2,
∴E1(-3,0);
当AC为边,平行四边形为ACFE时,则AE2∥CF2,同样可得AE2=CF2=2,则E2(1,0);
当AC为边,平行四边形为ACEF时,则点F和点C到x轴的距离相等,所以点F的纵坐标为2,
若y=2,则$\frac{2}{3}$x2-$\frac{4}{3}$x-2=2,
解得x1=1+$\sqrt{7}$,x2=1+$\sqrt{7}$,
则F3(1-$\sqrt{7}$,2),F4(1+$\sqrt{7}$,0),
∵点A向右平移1个单位,向下平移2个单位得到C点,
∴点F向右平移1个单位,向下平移2个单位得到E点,
∴E3(2-$\sqrt{7}$,0),E4(2+$\sqrt{7}$,0),
综上所述,满足条件的E点坐标为(-3,0),(1,0),(2-$\sqrt{7}$,0),(2+$\sqrt{7}$,0).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;会利用待定系数法求二次函数解析式;理解坐标与图形性质,掌握点平移的坐标规律;会利用三角函数的定义进行几何计算;能运用分类讨论的思想解决数学问题.

| A. | $\sqrt{-2}$ | B. | $\sqrt{0}$ | C. | $\sqrt{-(-2)}$ | D. | $\sqrt{(-1)^{2}}$ |
| A. | -32007 | B. | 32007 | C. | 1 | D. | -1 |
| A. | 2 与-$\frac{1}{2}$ | B. | -2与2 | C. | 2 与丨-2| | D. | $\frac{1}{2}$与-2 |
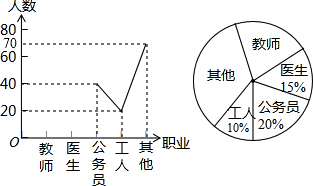 某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )| A. | 被调查的学生有200人 | |
| B. | 扇形图中公务员部分所对应的圆心角为72° | |
| C. | 若全校有2000名学生则喜欢教师职业的大约有400人 | |
| D. | 被调查的学生中喜欢其它职业的占40% |
| A. | 4.5,2 | B. | 4,6 | C. | 4,4 | D. | 3.5,4 |
| A. | “打开电视机,正在播《民生面对面》”是必然事件 | |
| B. | “一个不透明的袋中装有6个红球,从中摸出1个球是红球”是随机事件 | |
| C. | “概率为0.0001的事件”是不可能事件 | |
| D. | “在操场上向上抛出的篮球一定会下落”是确定事件 |
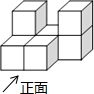 如图所示的几何体是由七个相同的小正方体组合而成的,它的左视图是( )
如图所示的几何体是由七个相同的小正方体组合而成的,它的左视图是( )