题目内容
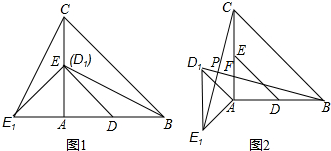
9.在Rt△ABC中,∠CAB=90°,AC=AB=6,D,E分别是AB,AC的中点,若等腰Rt△ADE绕点A逆时针旋转,得到Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.(1)如图1,当α=90°时,线段BD1的长等于3$\sqrt{5}$,线段CE1的长等于3$\sqrt{5}$;
(2)如图2,当α=135°时,设直线BD1与CA的交点为F,求证:BD1=CE1,且BD1⊥CE1;
(3)点P到AB所在直线的距离的最大值是$\frac{3+3\sqrt{3}}{2}$.
分析 (1)利用等腰直角三角形的性质结合勾股定理分别得出BD1的长和CE1的长;
(2)根据旋转的性质得出,∠D1AB=∠E1AC=135°,进而求出△D1AB≌△E1AC(SAS),即可得出答案;
(3)首先作PG⊥AB,交AB所在直线于点G,则D1,E1在以A为圆心,AD为半径的圆上,当BD1所在直线与⊙A相切时,直线BD1与CE1的交点P到直线AB的距离最大,
此时四边形AD1PE1是正方形,进而求出PG的长.
解答 解:
(1)∵∠CAB=90°,AC=AB=6,D,E分别是边AB,AC的中点,
∴AE=AD=3,
∵等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),
∴当α=90°时,AE1=3,∠E1AE=90°,
∴BD1=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,E1C=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$;
故答案为:3$\sqrt{5}$,3$\sqrt{5}$;
(2)证明:当α=135°时,如图2,连接CE1,
∵Rt△AD1E是由Rt△ADE绕点A逆时针旋转135°得到,
∴AD1=AE1,∠D1AB=∠E1AC=135°,
在△D1AB和△E1AC中
$\left\{\begin{array}{l}{A{D}_{1}=A{E}_{1}}\\{∠{D}_{1}AB=∠{E}_{1}AC}\\{AB=AC}\end{array}\right.$,
∴△D1AB≌△E1AC(SAS),
∴BD1=CE1,且∠D1BA=∠E1CA,
记直线BD1与AC交于点F,
∴∠BFA=∠CFP,
∴∠CPF=∠FAB=90°,
∴BD1⊥CE1;
(3)解:如图3,作PG⊥AB,交AB所在直线于点G,
∵D1,E1在以A为圆心,AD为半径的圆上,
∴当BD1所在直线与⊙A相切时,直线BD1与CE1的交点P到直线AB的距离最大,
此时四边形AD1PE1是正方形,PD1=3,则BD1=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
故∠ABP=30°,
则PB=3+3$\sqrt{3}$,
故点P到AB所在直线的距离的最大值为:PG=$\frac{3+3\sqrt{3}}{2}$,
故答案为:$\frac{3+3\sqrt{3}}{2}$.
点评 本题为三角形的综合应用,涉及到几何变换、全等三角形的判定和性质、等腰腰直角三角形的性质和勾股定理以及切线的性质等知识点.在(2)中注意三角形全等的应用,在(3)中根据题意得出PG的最长时P点的位置是解题关键.本题考查知识点较多,综合性很强,难度较大.

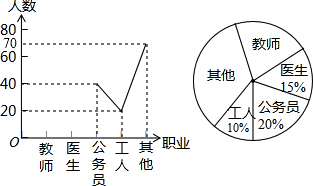 某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
某中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )| A. | 被调查的学生有200人 | |
| B. | 扇形图中公务员部分所对应的圆心角为72° | |
| C. | 若全校有2000名学生则喜欢教师职业的大约有400人 | |
| D. | 被调查的学生中喜欢其它职业的占40% |
| A. | -6 | B. | 6 | C. | 9 | D. | $\frac{1}{9}$ |
| A. | “打开电视机,正在播《民生面对面》”是必然事件 | |
| B. | “一个不透明的袋中装有6个红球,从中摸出1个球是红球”是随机事件 | |
| C. | “概率为0.0001的事件”是不可能事件 | |
| D. | “在操场上向上抛出的篮球一定会下落”是确定事件 |