题目内容
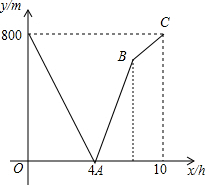
甲车从a地驶往b地，乙车从b地驶往a地，甲车的速度小于乙车的速度，两车同时出发，各自到达目的地后停止，设两车之间的距离为y（km），甲车行驶的时间为x（h），y与x的函数图象如图所示．（1）求出甲，乙两车的速度；
（2）求两车相遇后y与x的函数关系式．
考点：一次函数的应用
专题：
分析：（1）由函数图象先可以求出甲、乙的速度和，再求出甲的速度就可以求出乙的速度；
（2）根据乙的速度求出乙走完全程的时间，就可以求出B的坐标，由待定系数法就可以求出AB，BC的解析式．
（2）根据乙的速度求出乙走完全程的时间，就可以求出B的坐标，由待定系数法就可以求出AB，BC的解析式．
解答：解：（1）由题意，得，
甲车的速度为：800÷10=80km/h，
乙车的速度为：800÷4-80=120km/h．
答：甲，乙两车的速度分别为80km/h，120km/h；
（2）由题意，得
乙车走完全程的时间是：800÷120=
小时，
200×（
-4）=
，
∴B（
，
）．
当4＜x≤
时，设AB的解析式为y=kx+b，由题意，得
解得：
，
y=200x-800．
当
＜x≤10时，设BC的解析式为y=k1x+b1，由题意，得
，
解得：
，
y=80x．
综上所述：
y=
．
甲车的速度为：800÷10=80km/h，
乙车的速度为：800÷4-80=120km/h．
答：甲，乙两车的速度分别为80km/h，120km/h；
（2）由题意，得
乙车走完全程的时间是：800÷120=
| 20 |
| 3 |
200×（
| 20 |
| 3 |
| 1600 |
| 3 |
∴B（
| 20 |
| 3 |
| 1600 |
| 3 |
当4＜x≤
| 20 |
| 3 |
|
解得：
|
y=200x-800．
当
| 20 |
| 3 |
|
解得：
|
y=80x．
综上所述：
y=
|
点评：本题考查了行程问题的数量关系速度=路程÷时间的运用，速度和的运用，待定系数法求一次函数的解析式的运用，分段函数的运用，解答时正确理解函数图象的数据的意义是关键．
练习册系列答案
相关题目
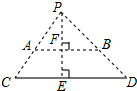电灯P在横杆AB的正上方，AB在灯光下的影子为CD，AB∥CD，AB=2m，CD=5m．
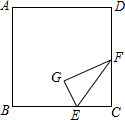如图，把正方形ABCD的一个角向上折，EF为折痕，点C落在点G处，测得AD=30cm，BE=20cm，∠BEG=60°，求折痕EF的长．
用直尺和圆规作图，保留作图痕迹，不写作法．
如图，△ACB为等腰直角三角形，AC⊥BC，AE∥BC，AF=AC，AM平分∠EAF．
一个花坛的形状如图所示，它的两端是半径相等的半圆，求：