题目内容
 如图,△ACB为等腰直角三角形,AC⊥BC,AE∥BC,AF=AC,AM平分∠EAF.
如图,△ACB为等腰直角三角形,AC⊥BC,AE∥BC,AF=AC,AM平分∠EAF.(1)求证:∠AMC=45°;
(2)求证:AM⊥MB.
考点:相似三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)设∠ACF=∠F=α,∠FAM=∠EAM=β;运用三角形的内角和定理证明α+β=45°,即可解决问题.
(2)证明∠ABC=∠AMC,得到A、C、B、M四点共圆,进而得到∠AMB+∠ACB=180°,即可解决问题.
(2)证明∠ABC=∠AMC,得到A、C、B、M四点共圆,进而得到∠AMB+∠ACB=180°,即可解决问题.
解答: 证明:(1)∵AC=AF,AM平分∠EAF,
证明:(1)∵AC=AF,AM平分∠EAF,
∴∠ACF=∠F(设为α),∠FAM=∠EAM(设为β);
∵AC⊥BC,AE∥BC,
∴∠CAE+∠ACB=180°,∠ACB=90°,
∴∠CAE=90°;
∵∠CAF+∠F+∠ACF=180°,
∴2(α+β)+90°=180°,
∴α+β=45°,∠AMC=α+β=45°.
(2)∵△ACB为等腰直角三角形,
∴∠ABC=45°,而∠AMC=45°,
∴∠ABC=∠AMC,
∴A、C、B、M四点共圆,
∴∠AMB+∠ACB=180°,而∠ACB=90°,
∴∠AMB=90°,AM⊥MB.
 证明:(1)∵AC=AF,AM平分∠EAF,
证明:(1)∵AC=AF,AM平分∠EAF,∴∠ACF=∠F(设为α),∠FAM=∠EAM(设为β);
∵AC⊥BC,AE∥BC,
∴∠CAE+∠ACB=180°,∠ACB=90°,
∴∠CAE=90°;
∵∠CAF+∠F+∠ACF=180°,
∴2(α+β)+90°=180°,
∴α+β=45°,∠AMC=α+β=45°.
(2)∵△ACB为等腰直角三角形,
∴∠ABC=45°,而∠AMC=45°,
∴∠ABC=∠AMC,
∴A、C、B、M四点共圆,
∴∠AMB+∠ACB=180°,而∠ACB=90°,
∴∠AMB=90°,AM⊥MB.
点评:该题主要考查了等腰直角三角形的性质及其应用问题;同时还渗透了对平行线的性质、三角形的内角和定理、四点共圆的判定等几何知识点的考查问题;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
将抛物线y=2x2向右平移1个单位,得到的抛物线是( )
| A、y=2x2+1 |
| B、y=2x2-1 |
| C、y=2(x+1) |
| D、y=2(x-1)2 |
 甲车从a地驶往b地,乙车从b地驶往a地,甲车的速度小于乙车的速度,两车同时出发,各自到达目的地后停止,设两车之间的距离为y(km),甲车行驶的时间为x(h),y与x的函数图象如图所示.
甲车从a地驶往b地,乙车从b地驶往a地,甲车的速度小于乙车的速度,两车同时出发,各自到达目的地后停止,设两车之间的距离为y(km),甲车行驶的时间为x(h),y与x的函数图象如图所示.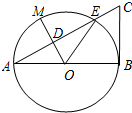 如图,以线段AB为直径的⊙O交线段AC于点E,点D是AE的中点,连接OD并延长交⊙O于点M,∠BOE=60°,cosC=
如图,以线段AB为直径的⊙O交线段AC于点E,点D是AE的中点,连接OD并延长交⊙O于点M,∠BOE=60°,cosC= 如图,在平面直角坐标系中,矩形OABC的对角线AC所在的直线的解析式为y=-
如图,在平面直角坐标系中,矩形OABC的对角线AC所在的直线的解析式为y=-