题目内容
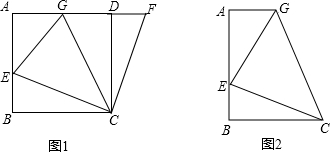
目前，瓜沥镇正在为小城市建设做着不懈努力，镇政府决定在新城区政府大楼前建设一块个长a米，宽b米的长方形草坪，并计划在该草坪场地上修筑宽都为2米的两条互相垂直的人行道（如图）．（1）用含a，b的代数式表示两条人行道的总面积；
（2）若a，b满足代数式
| a-b | ||||
|
| 6 |
| b |
| a-b | ||||
|
（3）若已知a：b值满足（2）的条件，并且四块草坪的面积之和为2204平方米，试求原长方形的长与宽各为多少米？
考点：一元二次方程的应用
专题：几何图形问题
分析：（1）用人行横道的长乘以宽后相加减去重合部分的面积即可；
（2）对等式两边的各项分母有理化后利用等式的性质化简即可确定比值；
（3）根据求得的比，设出矩形的长和宽，然后利用面积为2204即可求得原矩形的长和宽．
（2）对等式两边的各项分母有理化后利用等式的性质化简即可确定比值；
（3）根据求得的比，设出矩形的长和宽，然后利用面积为2204即可求得原矩形的长和宽．
解答：解：（1）∵两条人行横道的长分别为a米和b米，宽均为2米，
∴人行横道的面积为：2a+2b-4；
（2）等式两边同时分母有理化得：
+
=
×
-
+
，
整理得：2
=
×
，
∴a：b=3：2；
（3）∵a：b=3：2，
∴设a=3x，则b=2x，
根据题意得：（3x-2）（2x-2）=2204
解答：x=20或x=-
（舍去）
∴3x=60，2x=40，
答：原长方形的长与宽各为60米和40米．
∴人行横道的面积为：2a+2b-4；
（2）等式两边同时分母有理化得：
| a |
| b |
| 6 |
| b |
| a |
| b |
整理得：2
| a |
| 6 |
| b |
∴a：b=3：2；
（3）∵a：b=3：2，
∴设a=3x，则b=2x，
根据题意得：（3x-2）（2x-2）=2204
解答：x=20或x=-
| 55 |
| 3 |
∴3x=60，2x=40，
答：原长方形的长与宽各为60米和40米．
点评：本题考查了一元二次方程的应用的知识，正确的解答第二题是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
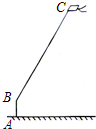周末，小强在文化广场放风筝．如图，小强为了计算风筝离地面的高度，他测得风筝的仰角为58°，已知风筝线BC的长为10米，小强的身高AB为1.55米．请你帮小强画出测量示意图，并计算出风筝离地面的高度（结果精确到0.1米）．（参考数据：sin58°=0.85，cos58°=0.53，tan58°=1.60）
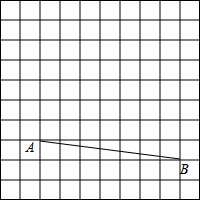在网格中每个小正方形的边长均为1，A、B两点在正方形的顶点上，
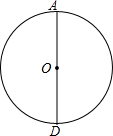在学习圆与正多边形时，马露、高静两位同学设计了一个画圆内接正三角形的方法：
如图，在平面直角坐标系xOy中，直线y=kx+b与x轴交于点A（1，0），与y轴交于点B（0，2）．
一辆轿车从甲地驶往乙地，到达乙地后返回甲地，速度是原来的1.5倍，共用t小时；一辆货车同时从甲地驶往乙地，到达乙地后停止．两车同时出发，匀速行驶．设轿车行驶的时间为x（h），两车到甲地的距离为y（km），两车行驶过程中y与x之间的函数图象如图．