题目内容
 如图,在平面直角坐标系xOy中,直线y=kx+b与x轴交于点A(1,0),与y轴交于点B(0,2).
如图,在平面直角坐标系xOy中,直线y=kx+b与x轴交于点A(1,0),与y轴交于点B(0,2).(1)求直线AB的表达式和线段AB的长;
(2)将△OAB绕点O逆时针旋转90°后,点A落到点C处,点B落到点D处,求线段AB上横坐标为a的点E在线段CD上的对应点F的坐标(用含a的代数式表示).
考点:一次函数综合题
专题:综合题
分析:(1)利用待定系数法可求出直线AB的解析式,利用勾股定理可得线段AB的长度.
(2)设点E的坐标为(a,-2a+2),根据旋转的性质即可得出点F的坐标.
(2)设点E的坐标为(a,-2a+2),根据旋转的性质即可得出点F的坐标.
解答:解:(1)将点A(1,0),点B(0,2)代入直线y=kx+b,得:
,
解得:
∴直线AB的解析式为y=-2x+2,
线段AB=
=
.
(2)∵E为线段AB上横坐标a的点,
∴第一象限的E(a,-2a+2),
根据题意F为E绕点O逆时针旋转90°后的对应点,
第二象限的F的坐标为(-|-2a+2|,|a|)
∴点F(2a-2,a).
|
解得:
|
∴直线AB的解析式为y=-2x+2,
线段AB=
| (1-0)2+(0-2)2 |
| 5 |
(2)∵E为线段AB上横坐标a的点,
∴第一象限的E(a,-2a+2),
根据题意F为E绕点O逆时针旋转90°后的对应点,
第二象限的F的坐标为(-|-2a+2|,|a|)
∴点F(2a-2,a).
点评:本题考查了一次函数的综合,涉及了待定系数法、勾股定理及旋转的性质,难度一般.

练习册系列答案
相关题目

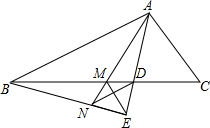 △ABC中,AD平分∠BAC,BE垂直AD交AD延长线于点E,M为BC中点,连接ME.
△ABC中,AD平分∠BAC,BE垂直AD交AD延长线于点E,M为BC中点,连接ME. 目前,瓜沥镇正在为小城市建设做着不懈努力,镇政府决定在新城区政府大楼前建设一块个长a米,宽b米的长方形草坪,并计划在该草坪场地上修筑宽都为2米的两条互相垂直的人行道(如图).
目前,瓜沥镇正在为小城市建设做着不懈努力,镇政府决定在新城区政府大楼前建设一块个长a米,宽b米的长方形草坪,并计划在该草坪场地上修筑宽都为2米的两条互相垂直的人行道(如图).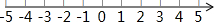 解不等式:7-x≤1-4(x-3),并把解集在所给数轴上表示出来.
解不等式:7-x≤1-4(x-3),并把解集在所给数轴上表示出来.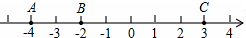
 如图,要得到AB∥CD,只需要添加一个条件,这个条件可以是
如图,要得到AB∥CD,只需要添加一个条件,这个条件可以是