题目内容
(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
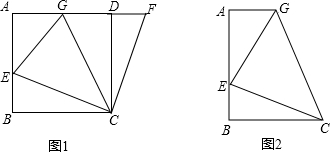
①试说明CE=CF;
②若G在AD上,且∠GCE=45°,则EG=BE+GD成立吗?为什么?
(2)运用(1)解答中所积累的经验和知识,完成下题:
如图2,在梯形ABCG中,AG∥BC(BC>AG),∠B=90°,AB=BC=6,E是AB上一点,且∠GCE=45°,BE=2,求EG的长.

①试说明CE=CF;
②若G在AD上,且∠GCE=45°,则EG=BE+GD成立吗?为什么?
(2)运用(1)解答中所积累的经验和知识,完成下题:
如图2,在梯形ABCG中,AG∥BC(BC>AG),∠B=90°,AB=BC=6,E是AB上一点,且∠GCE=45°,BE=2,求EG的长.
考点:全等三角形的判定与性质,正方形的性质
专题:
分析:(1)①根据正方形的性质可得BC=CD,再利用“边角边”证明△BCE和△DCF全等,根据全等三角形对应边相等可得CE=CF;
②根据全等三角形对应角相等可得∠BCE=∠DCF,再求出∠GCF=45°,从而得到∠GCF=∠GCE,再利用“边角边”证明△GCE和△GCF全等,根据全等三角形对应边相等可得EG=GF,然后根据GF=DF+GD代换即可得证;
(2)设EG=x,根据(1)的结论表示出AG,再求出AE,然后在Rt△AEG中,利用勾股定理列出方程求解即可.
②根据全等三角形对应角相等可得∠BCE=∠DCF,再求出∠GCF=45°,从而得到∠GCF=∠GCE,再利用“边角边”证明△GCE和△GCF全等,根据全等三角形对应边相等可得EG=GF,然后根据GF=DF+GD代换即可得证;
(2)设EG=x,根据(1)的结论表示出AG,再求出AE,然后在Rt△AEG中,利用勾股定理列出方程求解即可.
解答:(1)①证明:在正方形ABCD中,BC=CD,
在△BCE和△DCF中,
,
∴△BCE≌△DCF(SAS),
∴CE=CF;
②EG=BE+GD.
理由如下:∵△BCE≌△DCF,
∴∠BCE=∠DCF,
∵∠GCE=45°,
∴∠GCF=∠GCD+∠DCF=∠GCD+∠BCE=90°-45°=45°,
∴∠GCF=∠GCE,
在△GCE和△GCF中,
,
∴△GCE≌△GCF(SAS),
∴EG=GF,
∵GF=DF+GD,
∴EG=BE+GD;
(2)设EG=x,
由(1)可知,BE+(6-AG)=EG,
即2+(6-AG)=x,
∴AG=8-x,
又∵AE=AB-BE=6-2=4,
∴在Rt△AEG中,AE2+AG2=EG2,
即42+(8-x)2=x2,
解得x=5,
即EG=5.
在△BCE和△DCF中,
|
∴△BCE≌△DCF(SAS),
∴CE=CF;
②EG=BE+GD.
理由如下:∵△BCE≌△DCF,
∴∠BCE=∠DCF,
∵∠GCE=45°,
∴∠GCF=∠GCD+∠DCF=∠GCD+∠BCE=90°-45°=45°,
∴∠GCF=∠GCE,
在△GCE和△GCF中,
|
∴△GCE≌△GCF(SAS),
∴EG=GF,
∵GF=DF+GD,
∴EG=BE+GD;
(2)设EG=x,
由(1)可知,BE+(6-AG)=EG,
即2+(6-AG)=x,
∴AG=8-x,
又∵AE=AB-BE=6-2=4,
∴在Rt△AEG中,AE2+AG2=EG2,
即42+(8-x)2=x2,
解得x=5,
即EG=5.
点评:本题考查了全等三角形的判定与性质,正方形的性质,勾股定理的应用,熟练掌握三角形全等的判定方法并证明得到全等的条件∠GCF=∠GCE是解题的关键,(2)求出各边的长并利用勾股定理列出方程是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 目前,瓜沥镇正在为小城市建设做着不懈努力,镇政府决定在新城区政府大楼前建设一块个长a米,宽b米的长方形草坪,并计划在该草坪场地上修筑宽都为2米的两条互相垂直的人行道(如图).
目前,瓜沥镇正在为小城市建设做着不懈努力,镇政府决定在新城区政府大楼前建设一块个长a米,宽b米的长方形草坪,并计划在该草坪场地上修筑宽都为2米的两条互相垂直的人行道(如图). 如图,把△ABC向右平移5个方格,再绕点B的对应点顺时针方向旋转90°.
如图,把△ABC向右平移5个方格,再绕点B的对应点顺时针方向旋转90°.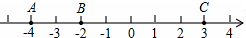
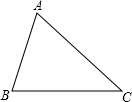 在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′B′C′(顶点A、C分别与A′、C′对应),当点C在线段CA的延长线上时,则AC′的长度为
在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′B′C′(顶点A、C分别与A′、C′对应),当点C在线段CA的延长线上时,则AC′的长度为