题目内容
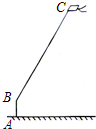周末，小强在文化广场放风筝．如图，小强为了计算风筝离地面的高度，他测得风筝的仰角为58°，已知风筝线BC的长为10米，小强的身高AB为1.55米．请你帮小强画出测量示意图，并计算出风筝离地面的高度（结果精确到0.1米）．（参考数据：sin58°=0.85，cos58°=0.53，tan58°=1.60）考点：解直角三角形的应用-仰角俯角问题
专题：
分析：根据题意画出图形，根据sin58°=
可求出CE的长，再根据CD=CE+ED即可得出答案．
| CE |
| BC |
解答：
解：如图，过点C作地面的垂线CD，垂足为D，过点B作BE⊥CD于E．
在Rt△CEB中，∵sin∠CBE=
，
∴CE=BC•sin58°=10×0.85≈8.5m，
∴CD=CE+ED=8.5+1.55=10.05≈10.1m，
答：风筝离地面的高度约为10.1m．
解：如图，过点C作地面的垂线CD，垂足为D，过点B作BE⊥CD于E．在Rt△CEB中，∵sin∠CBE=
| CE |
| BC |
∴CE=BC•sin58°=10×0.85≈8.5m，
∴CD=CE+ED=8.5+1.55=10.05≈10.1m，
答：风筝离地面的高度约为10.1m．
点评：本题考查的是解直角三角形的应用-仰角俯角问题，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
若有理数a和b在数轴上所表示的点分别在原点的右边和左边，则
-|a-b|等于（ ）
| b2 |
| A、a | B、-a |
| C、2b+a | D、2b-a |
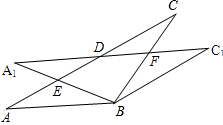如图，在等腰△ABC中，AB=BC，∠A=30°将△ABC绕点B顺时针旋转30°，得△A1BC1，A1B交AC于点E，A1C1分别交AC、BC于D、F两点．
已知：如图，在平面直角坐标系xOy中，抛物线
如图，已知∠1=52°，∠2=128°，∠C=∠D，探索∠A与∠F的数量关系，并说明理由．
目前，瓜沥镇正在为小城市建设做着不懈努力，镇政府决定在新城区政府大楼前建设一块个长a米，宽b米的长方形草坪，并计划在该草坪场地上修筑宽都为2米的两条互相垂直的人行道（如图）．