题目内容
5.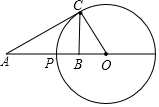 已知点P在线段AB上,点O在线段AB延长线上,以点O为圆心,OP为半径作圆,点C是圆O上的一点.
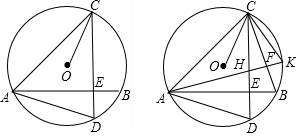
已知点P在线段AB上,点O在线段AB延长线上,以点O为圆心,OP为半径作圆,点C是圆O上的一点.(1)如图,如果AP=2PB,PB=BO,求证:△CAO∽△BCO;
(2)如果AP=m(m是常数,且m>1),BP=1,OP是OA、OB的比例中项,当点C在圆O上运动时,求AC:BC的值(结果用含m的式子表示).
分析 (1)根据夹角相等,对应边成比例可证;
(2)OP是OA,OB的比例中项,OC=OP,△CAO∽△BCO可得.
解答 (1)证明:∵AP=2PB=PB+BO=PO,
∴AO=2PO.
∴$\frac{AO}{PO}$=$\frac{PO}{BO}$=2,
∵PO=CO,
∴$\frac{AO}{OC}=\frac{OC}{OB}$.
∵∠COA=∠BOC,
∴△CAO∽△BCO;
(2)解:设OP=x,则OB=x-1,OA=x+m,
∵OP是OA,OB的比例中项,
∴x2=(x-1)(x+m),
∴x=$\frac{m}{m-1}$.
即OP=$\frac{m}{m-1}$,
∴OB=$\frac{1}{m-1}$,
∵OP是OA,OB的比例中项,即$\frac{OA}{OP}$=$\frac{OP}{OB}$,
∵OP=OC,
∴$\frac{AO}{OC}=\frac{OC}{OB}$.
设⊙O与线段AB的延长线相交于点Q,当点C与点P,点Q不重合时,
∵∠AOC=∠COB,
∴△CAO∽△BCO,
∴$\frac{AC}{BC}$=$\frac{OC}{OB}$,
∴$\frac{AC}{BC}$=$\frac{OC}{OB}$=$\frac{OP}{OB}$=m.
当点C与点P或点Q重合时,可得$\frac{AC}{BC}$=m,
∴当点C在圆O上运动时,AC:BC=m.
点评 本题考查了相似三角形的判定和性质,比例的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
10.下列说法正确的是( )
| A. | 三角形的外切圆有且只有一个 | |
| B. | 三角形的外心到这个三角形的三边距离相等 | |
| C. | 相等的圆心角所对的弧相等 | |
| D. | 等弧所对的圆心角相等 |
14.如果m÷n=12.其中m,n都是正整数,那么它们的最小公倍数是( )
| A. | m | B. | n | C. | 12 | D. | m与n的积 |
 如图,共有9个长方形.
如图,共有9个长方形.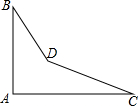 如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?
如图,是一个零件的形状,按规定∠A应等于90°,∠B与∠C分别是32°和27°,检测工人量得∠BDC=150°,问该零件是否合格?为什么?