题目内容
16.当x≠0时,分式$\frac{-{x}^{2}}{{x}^{2}+1}$的值为负数;当x>-2时,分式$\frac{x+2}{{x}^{2}}$的值为正数.分析 由分式的分母恒大于0,分式的值为负数,得到分子小于0,即可求出x的范围;由分式的分母恒大于等于0,分式的值为正数,得到分子大于0,即可求出x的范围.
解答 解:∵x2+1>0,
∴-x2<0,
∴当x≠0时,分式$\frac{-{x}^{2}}{{x}^{2}+1}$的值为负数;
∵x2>0,
∴x+2>0,
∴当x>-2时,分式$\frac{x+2}{{x}^{2}}$的值为正数;
故答案为≠0;>-2.
点评 本题考查了分式的值以及解一元一次不等式,掌握分式值为0的条件和分式有意义的条件是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
(1)根据上表的数据,你能用t表示Q吗?试一试;
(2)汽车行驶6h后,油箱中的剩余油量是多少?
(3)若汽车油箱中剩余油量为52L,则汽车行驶了多少小时?
(4)若该种汽车油箱只装了36L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗,为什么?
| 汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
(2)汽车行驶6h后,油箱中的剩余油量是多少?
(3)若汽车油箱中剩余油量为52L,则汽车行驶了多少小时?
(4)若该种汽车油箱只装了36L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗,为什么?
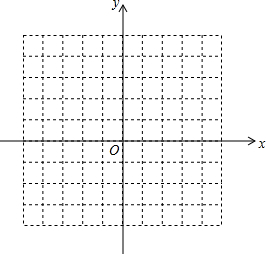 如图,已知A(-3,-3),B(-2,-1),C(-1,-3)是直角坐标平面上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1,-3)是直角坐标平面上三点.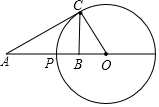 已知点P在线段AB上,点O在线段AB延长线上,以点O为圆心,OP为半径作圆,点C是圆O上的一点.
已知点P在线段AB上,点O在线段AB延长线上,以点O为圆心,OP为半径作圆,点C是圆O上的一点.