题目内容
13.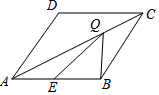 如图,在边长为2的菱形ABCD中,∠DAB=60°,E是AB边上的一点,且AE=1,点Q为对角线AC上的动点,则△BEQ周长的最小值为1+$\sqrt{3}$.
如图,在边长为2的菱形ABCD中,∠DAB=60°,E是AB边上的一点,且AE=1,点Q为对角线AC上的动点,则△BEQ周长的最小值为1+$\sqrt{3}$.
分析 作点E关于AC的对称点,E′,连结E′Q,E′B,E′B.先利用轴对称的性质证明QE′=QE,则QE+QB=QE′+QB,当点E′、Q、B在一条直线上时,△QEB的周长最小,然后再证明△ABE′为直角三角形,从而可求得E′B的值,最后依据△QEB的周长=BE+QE+QB=BE+BE′求解即可.
解答 解:作点E关于AC的对称点,E′,连结E′Q,E′B,E′B.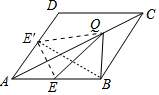
∵ABCD为菱形,
∴点E′在AD上.
∵点E与点E′关于AQ对称,
∴QE′=QE.
∵EB为定值,
∴当EQ与BQ和最小时,△QEB的周长最小.
∵QE+QB=QE′+QB,
∴当点E′、Q、B在一条直线上时,△QEB的周长最小.
∵AE=AE′,∠DAB=60°,
∴△AEE′为等边三角形.
∴∠E′EA=∠AE′E=60°,EE′=AE.
∵AB=2,AE=1,
∴EB=AE,
∴EE′=EB.
∴∠EE′B=∠EBE′=$\frac{1}{2}$∠E′EA=30°.
∴∠AE′B=90°.
∴E′B=$\sqrt{A{B}^{2}-AE{′}^{2}}$=$\sqrt{3}$.
∴△QEB的周长的最小值=1+$\sqrt{3}$.
故答案为:1$+\sqrt{3}$.
点评 本题主要考查的是轴对称路经最短、菱形的性质、等边三角形的判定和性质,明确当当点E′、Q、B在一条直线上时,△QEB的周长最小时解题的关键.

练习册系列答案
相关题目
3.如图,边长为(m+5)的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为5,则另一边长是( )
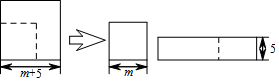

| A. | m+3 | B. | m+5 | C. | 2m+5 | D. | 2m+10 |
4. 如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
 如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )
如图,直角三角形三边向外作正方形,字母A所代表的正方形的面积为( )| A. | 4 | B. | 8 | C. | 16 | D. | 64 |
8.下列图形中,是中心对称但不是轴对称的图形是( )
| A. |  等边三角形 | B. |  正方形 | C. |  圆 | D. |  平等四边形 |
2.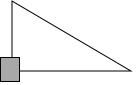 如图所示,小亮数学书上的直角三角形的直角处被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,小亮画出这个三角形的依据是( )
如图所示,小亮数学书上的直角三角形的直角处被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,小亮画出这个三角形的依据是( )
 如图所示,小亮数学书上的直角三角形的直角处被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,小亮画出这个三角形的依据是( )
如图所示,小亮数学书上的直角三角形的直角处被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,小亮画出这个三角形的依据是( )| A. | HL | B. | SAS或AAS | C. | ASA | D. | SSS |