题目内容
5.已知直线y=kx+6与坐标轴所围成的图形的面积为18,则k=±1.分析 先求出直线与坐标轴的交点,再由三角形的面积公式即可得出结论.
解答 解:直线y=kx+6与y轴的交点是(0,6)与x轴的交点是(-$\frac{6}{k}$,0)
∵直线y=kx+6与坐标轴所围图形的面积为18,
∴$\frac{1}{2}$×6×|-$\frac{6}{k}$|=18,|-$\frac{6}{k}$|=6,
∴-$\frac{6}{k}$=6或-$\frac{6}{k}$=-6,解得k=-1或k=1.
故答案为:±1.
点评 本题考查的是一次函数图象上点的坐标特点,熟知坐标轴上点的坐标特点是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
点A(x1,y1)、B(x2,y2)在函数的图象上,则当x1<x2<2时,y1与y2的大小关系正确的是( )
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | … |
| A. | y1≥y2 | B. | y1≤y2 | C. | y1>y2 | D. | y1<y2 |
14.将正六边形绕其对称中心旋转后,恰好能与原来的正六边形重合,那么旋转的角度至少是 ( )
| A. | 120° | B. | 60° | C. | 45° | D. | 30° |
15.在数轴上,表示数a的点到原点的距离是5个单位长度,数b是-$\frac{1}{3}$的倒数,则a+b=( )
| A. | 2或8 | B. | 2或-8 | C. | -2或8 | D. | -2或-8 |
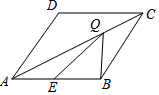 如图,在边长为2的菱形ABCD中,∠DAB=60°,E是AB边上的一点,且AE=1,点Q为对角线AC上的动点,则△BEQ周长的最小值为1+$\sqrt{3}$.
如图,在边长为2的菱形ABCD中,∠DAB=60°,E是AB边上的一点,且AE=1,点Q为对角线AC上的动点,则△BEQ周长的最小值为1+$\sqrt{3}$.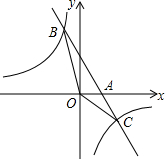 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$相交于B(-1,5),C($\frac{5}{2}$,d)两点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$相交于B(-1,5),C($\frac{5}{2}$,d)两点.