题目内容
17.从2开始,连续偶数相加,它们和的情况如下表:加数的个数和.1.2=1×2.
2.2+4=6=2×3.
3.2+4+6=12=3×4.
4.2+4+6+8=20=4×5
…观察上面的式子有怎样的规律,并用你发现的规律来计算:
(1)2+4+6+8+…+202
(2)126+128+130+…+300.
分析 (1)结合案例发现“后面乘法算式中第一个因数为前面加法算式中加数的个数,后一个因数为前面加法算式中首尾两数的平均数”规律,结合规律即可得出结论;
(2)结合案例发现“后面乘法算式中第一个因数为前面加法算式中加数的个数,后一个因数为前面加法算式中首尾两数的平均数”规律,将原始变形为两个算式相减的形式,再结合规律即可得出结论.
解答 解:观察给定的算式,可以发现后面乘法算式中第一个因数为前面加法算式中加数的个数,后一个因数为前面加法算式中首尾两数的平均数.
(1)结合发现规律可知:
2+4+6+8+…+202=$\frac{202}{2}$×$\frac{202+2}{2}$=101×102=10302.
(2)结合发现规律可知:126+128+130+…+300,
=(2+4+6+8+…+300)-(2+4+6+…+124),
=$\frac{300}{2}$×$\frac{300+2}{2}$-$\frac{124}{2}$×$\frac{124+2}{2}$,
=150×151-62×63,
=22650-3906,
=18744.
点评 本题考查了数字的变化,解题的关键是发现“后面乘法算式中第一个因数为前面加法算式中加数的个数,后一个因数为前面加法算式中首尾两数的平均数”这一规律.本题属于中档题,难度不大,但是在规律的叙述时,部分同学会感觉到无话可说,这就要教师们在日常教学中引导孩子们会用数学的语言来叙述各项问题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
5.用代入法解方程组$\left\{\begin{array}{l}2x+3y=7\\ 5x-y=9\end{array}\right.$先消去未知数( )最简便.
| A. | x | B. | y | ||
| C. | 两个中的任何一个都一样 | D. | 无法确定 |
12.若(a-1)2+|b-2|=0,则(a-b)2016的值是( )
| A. | -1 | B. | 1 | C. | 0 | D. | 2016 |
7.不等式组$\left\{\begin{array}{l}x>-2\\ x>a.\end{array}\right.$的解集是x>a,则a的取值范围是( )
| A. | a<-2 | B. | a=-2 | C. | a>-2 | D. | a≥-2 |
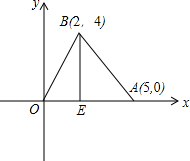 如图,在平面直角坐标系中,A(5,0),B(2,4),AB=5,BE垂直于x轴,垂足为点E,动点P从点A出发以3个单位/s的速度沿射线AB运动,动点Q从点O出发,在折线OA-AB上运动,在线段OA上以每秒5个单位速度运动,在AB上以每秒3个单位的速度,运动时间为t秒,若P、Q同时出发,点Q停止,点P随之停止运动.
如图,在平面直角坐标系中,A(5,0),B(2,4),AB=5,BE垂直于x轴,垂足为点E,动点P从点A出发以3个单位/s的速度沿射线AB运动,动点Q从点O出发,在折线OA-AB上运动,在线段OA上以每秒5个单位速度运动,在AB上以每秒3个单位的速度,运动时间为t秒,若P、Q同时出发,点Q停止,点P随之停止运动.