题目内容
3.我们把a、b、c三个数的中位数记作Z|a,b,c|,直线y=kx+$\frac{1}{2}$(k>0)与函数y=Z|x2-1,x+1,-x+1|的图象有且只有2个交点,则k的取值为$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.分析 画出函数y=Z|x2-1,x+1,-x+1|的图象,要使直线y=kx+$\frac{1}{2}$(k>0)与函数y=Z|x2-1,x+1,-x+1|的图象有且只有2个交点,只需直线经过(2,3)和经过(2,$\frac{1}{2}$)之间.
解答 解: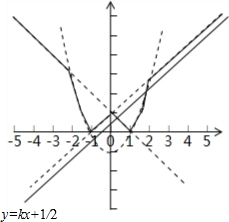 函数y=Z|x2-1,x+1,-x+1|的图象如图所示
函数y=Z|x2-1,x+1,-x+1|的图象如图所示
∵直线y=kx+$\frac{1}{2}$(k>0)与函数y=Z|x2-1,x+1,-x+1|的图象有且只有2个交点,
当直线y=kx+$\frac{1}{2}$(k>0)经过点(2,3)时,则3=2k+$\frac{1}{2}$,
解得k=$\frac{5}{4}$,
当直线y=kx+$\frac{1}{2}$(k>0)经过点(-1,0)时,k=$\frac{1}{2}$,
当k=1时,平行于y=x+1,与函数y=Z|x2-1,x+1,-x+1|的图象也有且仅有两个交点;
∴直线y=kx+$\frac{1}{2}$(k>0)与函数y=Z|x2-1,x+1,-x+1|的图象有且只有2个交点,则k的取值为$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.
故答案为$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.
点评 本题考查了一次函数的性质以及中位数的概念,数形结合思想的应用是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.在平面直角坐标中,已知点P(a,5)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
| A. | (-a,5) | B. | (a,-5) | C. | (-a+2,5) | D. | (-a+4,5) |
18.袋子中装有10个黑球、1个白球,它们除颜色外无其他差别,随机从袋子中摸出一个球,则( )
| A. | 这个球一定是黑球 | |
| B. | 摸到黑球、白球的可能性的大小一样 | |
| C. | 这个球可能是白球 | |
| D. | 事先能确定摸到什么颜色的球 |
8.将抛物线y=3x2先向左平移一个单位,再向上平移一个单位,两次平移后得到的抛物线解析式为( )
| A. | y=3(x+1)2+1 | B. | y=3(x+1)2-1 | C. | y=3(x-1)2+1 | D. | y=3(x-1)2-1 |
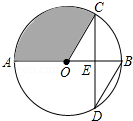 如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分的面积为12π.
如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分的面积为12π.