题目内容
15.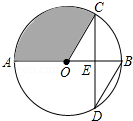 如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分的面积为12π.
如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分的面积为12π.
分析 根据题意得出△COB是等边三角形,进而得出CD⊥AB,再利用垂径定理以及锐角三角函数关系得出CO的长,进而结合扇形面积求出答案.
解答 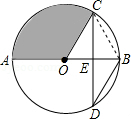 解:连接BC,
解:连接BC,
∵∠CDB=30°,
∴∠COB=60°,∴∠AOC=120°,
又∵CO=BO,
∴△COB是等边三角形,
∵E为OB的中点,
∴CD⊥AB,
∵CD=6$\sqrt{3}$,
∴EC=3$\sqrt{3}$,
∴sin60°×CO=3$\sqrt{3}$,
解得:CO=6,
故阴影部分的面积为:$\frac{120π×{6}^{2}}{360}$=12π.
故答案为:12π.
点评 此题主要考查了垂径定理以及锐角三角函数和扇形面积求法等知识,正确得出CO的长是解题关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
5.在(-1)2015,(-1)2016,-22,(-3)2这四个数中,最大的数与最小的数的和为( )
| A. | 6 | B. | 8 | C. | -5 | D. | 5 |
10. 将一副三角板按如图方式摆放在一起,若∠2=30°10′,则∠1的度数等于( )
将一副三角板按如图方式摆放在一起,若∠2=30°10′,则∠1的度数等于( )
 将一副三角板按如图方式摆放在一起,若∠2=30°10′,则∠1的度数等于( )
将一副三角板按如图方式摆放在一起,若∠2=30°10′,则∠1的度数等于( )| A. | 30°10′ | B. | 60°10′ | C. | 59°50′ | D. | 60°50′ |
7.若△ABC与△DEF相似,相似比为2:3,则这两个三角形的面积比为( )
| A. | 2:3 | B. | 3:2 | C. | 4:9 | D. | 9:4 |