��Ŀ����
��ͼ1����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-1��0������3��0������ͬʱ����A��B����ƽ��2����λ��������ƽ��1����λ���õ���A��B�Ķ�Ӧ��ֱ���C��D������AC��BD��CD��
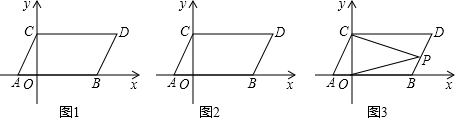
��1�����C��D�����꼰�ı���ABDC�����S�ı���ABCD��
��2����y�����Ƿ���ڵ�P������PA��PB��ʹS��PAB=S�ı���ABCD�������������ĵ㣬�����P�����ꣻ�������ڣ���˵�����ɣ�����ͼ2��
��3����P���߶�BD�ϵ�һ�����㣬����PC��PO������P��BD���ƶ�ʱ������B��D�غϣ��������н��ۣ�����ͼ3����
��
��ֵ���䣻��
��ֵ���䣻��S��CPD+S��OPB��ֵ���Ե���
����S��CPD+S��OPB��ֵ���Ե���
��
���Ͻ�������ȷ���ǣ� ��

��1�����C��D�����꼰�ı���ABDC�����S�ı���ABCD��
��2����y�����Ƿ���ڵ�P������PA��PB��ʹS��PAB=S�ı���ABCD�������������ĵ㣬�����P�����ꣻ�������ڣ���˵�����ɣ�����ͼ2��
��3����P���߶�BD�ϵ�һ�����㣬����PC��PO������P��BD���ƶ�ʱ������B��D�غϣ��������н��ۣ�����ͼ3����
��
| ��DCP+��CPO |
| ��BOP |
| ��DCP+��BOP |
| ��CPO |
| 5 |
| 2 |
| 13 |
| 4 |
���Ͻ�������ȷ���ǣ�
���㣺������ͼ������,�����ε����,������ͼ�α仯-ƽ��
ר�⣺
��������1����������ƽ�ƺ�����ӣ�����ƽ���������д����C��D�����꼴�ɣ��ٸ���ƽ���ı��ε������ʽ��ʽ���㼴�ɵý⣻
��2�����������ε�������S��PAB=S�ı���ABCDʱ��P��AB�ľ��룬��д��P�����꼴�ɣ�
��3������P��PE��CD��������ֱ��ƽ�У��ڴ�����ȿɵá�DCP=��CPE������ƽ�й����ɵ�PE��AB���ٸ�����ֱ��ƽ�У��ڴ�����ȿɵá�BOP=��OPE��Ȼ�������DCP+��BOP=��CPE+��OPE=��CPO���������ֵ���ɣ���������ֵ�����ó��𰸣�
��2�����������ε�������S��PAB=S�ı���ABCDʱ��P��AB�ľ��룬��д��P�����꼴�ɣ�
��3������P��PE��CD��������ֱ��ƽ�У��ڴ�����ȿɵá�DCP=��CPE������ƽ�й����ɵ�PE��AB���ٸ�����ֱ��ƽ�У��ڴ�����ȿɵá�BOP=��OPE��Ȼ�������DCP+��BOP=��CPE+��OPE=��CPO���������ֵ���ɣ���������ֵ�����ó��𰸣�
����⣺��1���ߵ�A��B������ֱ�Ϊ��-1��0������3��0����
��ͬʱ����A��B����ƽ��2����λ��������ƽ��1����λ���õ���A��B�Ķ�Ӧ��ֱ���C��D��
��C��0��2����D��4��2����
�ı���ABCD�����=��3+1����2=8��
��2����S��PAB=S�ı���ABCDʱ��P��AB�ľ���Ϊh��
��
����3+1��h=8��
���h=4��
��ҪʹS��PAB=S�ı���ABCD�����P������Ϊ��0��4������0��-4����
��3������P��PE��CD��
���DCP=��CPE��
��AB��CD��
��PE��AB��
���BOP=��OPE��
���DCP+��BOP=��CPE+��OPE=��CPO��
��
=1��ֵ���䣬��ȷ��
ͬ���ɵó�����
��ֵ���䣬����
�۵�P����D��ʱ��S��CPD+S��OPB��ֵ��С����ʱS��CPD+S��OPB=
��3��2=3����S��CPD+S��OPB�����Ե���
����ѡ�����
��
��3��
��S��CPD+S��OPB��ֵ���Ե���
�����ѡ����ȷ��
�ʴ�Ϊ���ڢܣ�
��ͬʱ����A��B����ƽ��2����λ��������ƽ��1����λ���õ���A��B�Ķ�Ӧ��ֱ���C��D��
��C��0��2����D��4��2����
�ı���ABCD�����=��3+1����2=8��
��2����S��PAB=S�ı���ABCDʱ��P��AB�ľ���Ϊh��
��
| 1 |
| 2 |
���h=4��
��ҪʹS��PAB=S�ı���ABCD�����P������Ϊ��0��4������0��-4����

��3������P��PE��CD��
���DCP=��CPE��
��AB��CD��
��PE��AB��
���BOP=��OPE��
���DCP+��BOP=��CPE+��OPE=��CPO��
��
| ��DCP+��BOP |
| ��CPO |
ͬ���ɵó�����
| ��DCP+��CPO |
| ��BOP |
�۵�P����D��ʱ��S��CPD+S��OPB��ֵ��С����ʱS��CPD+S��OPB=
| 1 |
| 2 |
| 5 |
| 2 |
��
| 13 |
| 4 |
��S��CPD+S��OPB��ֵ���Ե���
| 13 |
| 4 |
�ʴ�Ϊ���ڢܣ�
���������⿼����������ͼ�����ʣ�ƽ���ߵ����ʣ������ε������������ͼ�α仯-ƽ�ƣ���Ǹ������ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
��֪��Pλ��x���Ϸ�����x��ľ���Ϊ3����y��ľ���Ϊ4�����P����Ϊ��������
| A����4��3�� |
| B����3��4�� |
| C����4��3����-4��3�� |
| D����3��4����-3��4�� |
��ʵ��-2��
��
����0.101001000����-
�У��������ĸ����У�������
| 1 |
| 3 |
| 5 |
| 9 |
| A��2 | B��3 | C��4 | D��5 |
����x2•y2��-xy3��2�Ľ���ǣ�������
| A��x5y10 |
| B��x4y8 |
| C��-x5y8 |
| D��x6y12 |
 ��֪��������ʽ�Ľ⼯����������ͼ����ô����⼯Ϊ��������
��֪��������ʽ�Ľ⼯����������ͼ����ô����⼯Ϊ��������| A��x��-1 | B��x��2 |
| C��-1��x��2 | D��x��-1 |
 �Ķ����ϣ�Ȼ������Ӧ�������ڲ�ȫ֤�����̻���д���ɣ�
�Ķ����ϣ�Ȼ������Ӧ�������ڲ�ȫ֤�����̻���д���ɣ�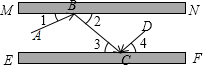 ��ͼ��MN��EF�����滥��ƽ�еľ��棬���ݾ��淴����ɣ���һ������AB���䵽����MN�ϣ��������ΪBC����һ���С�1=��2���Ը�����һ���ɣ�
��ͼ��MN��EF�����滥��ƽ�еľ��棬���ݾ��淴����ɣ���һ������AB���䵽����MN�ϣ��������ΪBC����һ���С�1=��2���Ը�����һ���ɣ� ��ͼ��ֱ��AC��BD��ֱ��AB�ֱ��������ཻ��A��B������ֱ�߰�ƽ��ֳɢ٢ڢۢܢݢ��������֣�ÿ�����ֲ������߽磩��������P����ij������ʱ������PA��PB�����ɡ�PAC����APB����PBD�����ǣ�
��ͼ��ֱ��AC��BD��ֱ��AB�ֱ��������ཻ��A��B������ֱ�߰�ƽ��ֳɢ٢ڢۢܢݢ��������֣�ÿ�����ֲ������߽磩��������P����ij������ʱ������PA��PB�����ɡ�PAC����APB����PBD�����ǣ�