题目内容
15.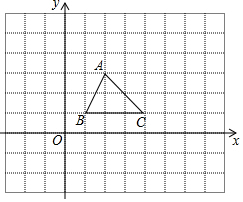 如图,在边长为1个单位长度的小正方形网格中,
如图,在边长为1个单位长度的小正方形网格中,(1)画出△ABC关于直线x=1的对称△A1B1C1.
(2)画出△ABC关于C点顺时针旋转90°的△A2B2C2.
(3)设P、Q两点分别是△ABC和△A1B1C1两对应点,已知P点坐标为(m,n),写出点Q的坐标.
分析 (1)分别作出点A、C关于x=1的对称点,顺次连接即可得;
(2)分别作出点A、B关于C点顺时针旋转90°所得对应点,再顺次连接即可得;
(3)根据轴对称的性质求解可得.
解答 解:(1)如图,△A1B1C1即为所求;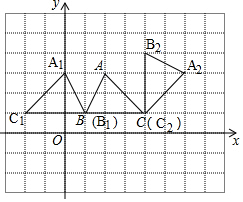
(2)如图,△A2B2C2即为所求;
(3)∵P、Q两点分别是△ABC和△A1B1C1两对应点,且△ABC与△A1B1C1关于直线x=1的对称,
∴P、Q两点的纵坐标相等,点Q的横坐标满足$\frac{x+m}{2}$=1,即x=2-m,
∴点Q的坐标为(2-m,n).
点评 本题主要考查作图-轴对称变换、旋转变换,熟练掌握轴对称变换、旋转变换的定义和性质是解题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
5.一元二次方程x2-x-1=0和2x2-6x+5=0,这两个方程的所有实数根之和为( )
| A. | 4 | B. | -4 | C. | -6 | D. | 1 |




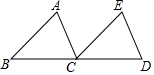 如图所示,△ECD是△ABC经过平移得到的,∠A=70°,∠B=40°,求∠ACE和∠D的度数.
如图所示,△ECD是△ABC经过平移得到的,∠A=70°,∠B=40°,求∠ACE和∠D的度数. 如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.
如图,在网格图中,每格是边长为1的正方形,四边形ABCD的顶点均为格点.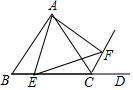 如图,在等边△ABC中,AB=4,点E在BC边上,将射线AE绕点A逆时针旋转60°,与△ABC的外角∠ACD的平分线交于点F,连接AF.设BE=x,△AEF的面积为y,则y与x之间的函数关系式为y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$.
如图,在等边△ABC中,AB=4,点E在BC边上,将射线AE绕点A逆时针旋转60°,与△ABC的外角∠ACD的平分线交于点F,连接AF.设BE=x,△AEF的面积为y,则y与x之间的函数关系式为y=$\frac{\sqrt{3}}{4}$x2-$\sqrt{3}$x+4$\sqrt{3}$.