题目内容

1．矩形纸片ABCD中，AD=10，AB=a（5＜a＜10）
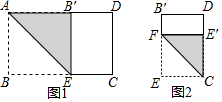
第1次操作：把该矩形的短边掀起，按图1那样折叠，使点B落在AD边上的B′处，折痕为AE，沿EB′剪下，剩下一个矩形B′ECD，此时ABEB′是正方形，B′D=10-a；
第二次操作：把矩形B′ECD的短边掀起，按图2那样折叠，使点E落在CD边上的E′处，折痕为CF，沿FE剪下，剩下一个矩形B′FE′D，此时E′D=（用含a的代数式表示）…
第n次操作后，剩下的矩形为正方形，则操作停止．
若n=3，则a=2或$\frac{15}{2}$．

分析 首先根据题意可得可知当10＜a＜20时，第一次操作后剩下的矩形的长为a，宽为10-a，第二次操作时正方形的边长为10-a，第二次操作以后剩下的矩形的两边分别为10-a，2a-10．然后分别从10-a＞2a-10与10-a＜2a-10去分析求解，即可求得答案．

解答 解：由题意可知当5＜a＜10时，第一次操作后剩下的矩形的长为a，宽为10-a，
所以第二次操作时剪下正方形的边长为10-a，第二次操作以后剩下的矩形的两边分别为10-a，2a-10；
∴E′D=2a-10；
此时，分两种情况：
①如果10-a＞2a-10，即a＜$\frac{20}{3}$，那么第三次操作时正方形的边长为2a-10．
则2a-10=（10-a）-（2a-10），解得a=6；
②如果10-a＜2a-10，即a＞$\frac{20}{3}$，那么第三次操作时正方形的边长为10-a．
则10-a=（2a-10）-（10-a），解得a=$\frac{15}{2}$．
∴当n=3时，a的值为2或$\frac{15}{2}$．
故答案为：2或$\frac{15}{2}$．

点评 此题考查了折叠的性质与矩形的性质．此题难度较大，注意掌握数形结合思想、分类讨论思想与方程思想的应用，注意折叠中的对应关系．

练习册系列答案
相关题目
11．已知x、y为正数，且|x2-4|与$\sqrt{{y}^{2}-3}$互为相反数，如果以x、y的长为直角边作直角三角形，那么以这个直角三角形的斜边为边长的正方形的面积为（　　）
A．5B．25C．7D．15
12．在半径为20的⊙O中，弦AB=32，点P在弦AB上，且OP=15，则AP=7或25．
9．威立到小吃店买水饺，他身上带的钱恰好等于15粒虾仁水饺或20粒韭菜水饺的价钱，若威立先买了9粒虾仁水饺，则他身上剩下的钱恰好可买多少粒韭菜水饺（　　）
A．6B．8C．9D．12
16．先化简，再求值：（a+b）2-2a（b+1）-a2b÷b，其中a=$\frac{1}{2}$，b=$\sqrt{3}$．
6．【知识链接】
（1）有理化因式：两个含有根式的非零代数式相乘，如果它们的积不含有根式，那么这两个代数式相互叫做有理化因式．
例如：$\sqrt{2}$的有理化因式是$\sqrt{2}$；1-$\sqrt{{x}^{2}+2}$的有理化因式是1+$\sqrt{{x}^{2}+2}$．
（2）分母有理化：分母有理化又称“有理化分母”，也就是把分母中的根号化去．指的是如果代数式中分母有根号，那么通常将分子、分母同乘以分母的有理化因式，达到化去分母中根号的目的．如：
$\frac{1}{1+\sqrt{2}}$=$\frac{1×（\sqrt{2}-1）}{（\sqrt{2}+1）（\sqrt{2}-1）}$=$\sqrt{2}$-1，$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×（\sqrt{3}-\sqrt{2}）}{（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）}$=$\sqrt{3}$-$\sqrt{2}$．
【知识理解】
（1）填空：2$\sqrt{x}$的有理化因式是$\sqrt{x}$；
（2）直接写出下列各式分母有理化的结果：
①$\frac{1}{\sqrt{7}+\sqrt{6}}$=$\sqrt{7}$-$\sqrt{6}$；②$\frac{1}{3\sqrt{2}+\sqrt{17}}$=3$\sqrt{2}$-$\sqrt{17}$．
【启发运用】
（3）计算：$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{2+\sqrt{3}}$+…+$\frac{1}{\sqrt{n+1}+\sqrt{n}}$．
13．完成下面的证明．
（1）如图（1），AB∥CD，CB∥DE．求证：∠B+∠D=180°．
证明：∵AB∥CD，
∴∠B=∠C①（两直线平行，内错角相等②）；
∵CB∥DE，
∴∠C+∠D=180°（两直线平行，同旁内角互补③）．
∴∠B+∠D=180°．
（2）如图（2），∠ABC=∠A′B′C′，BD，B′D′分别是∠ABC，∠A′B′C′的平分线．
求证∠1=∠2．
证明：∵BD，B′D′分别是∠ABC，∠A′B′C′的平分线，
∴∠1=$\frac{1}{2}$∠ABC，∠2=$\frac{1}{2}$∠A'B'C'④（⑤角平分线的定义）．
又∠ABC=∠A′B′C′，
∴$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠A′B′C′．
∴∠1=∠2（等量代换⑥）．
10．林甸某中学开展了一项为贫困学生助学活动，号召学生自愿捐款．已知七年级捐款总额为4800元，八年级捐款总额为5000元，八年级捐款人数比七年级多20人，而且两个年级人均捐款额恰好相等，求两个年级捐款总人数．
11．解不等式组$\left\{\begin{array}{l}{1-x＞-2①}\\{2x+3≥x-1②}\end{array}\right.$
请结合题意填空，完成本题的解答．
（Ⅰ）解不等式①，得x＜3；
（Ⅱ）解不等式②，得x≥-4；
（Ⅲ）把不等式①和②的解集在数轴上表示出来：
（Ⅳ）原不等式组的解集为-4≤x＜3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网