题目内容
 如图,锐角△ABC中,BD是∠ABC的角平分线,M、N分别是BD、BC线段上运动的点,S△ABC=8,AB=4,求:MN+MC的最小值是多少?
如图,锐角△ABC中,BD是∠ABC的角平分线,M、N分别是BD、BC线段上运动的点,S△ABC=8,AB=4,求:MN+MC的最小值是多少?考点:轴对称-最短路线问题
专题:
分析:因为BD是∠ABC的角平分线,设N关于BD的对称点为R,由于为锐角三角形,则R必在AB上,作AB边上的高CE,E在线段AB上,连接CR交AD于M,则MN=MR,CM+MN=CM+MR=CR,在直角三角形CER中,CR是斜边,CE是直角边,所以CR最小值是和CE重合即为三角形ABC的AB边上的高线,利用面积公式求出高线CE即可.
解答: 解:设N关于AB的对称点为R,由于为锐角三角形,则R必在AB上,作AB边上的高CE,E在线段AB上,连接CR交AD于M,
解:设N关于AB的对称点为R,由于为锐角三角形,则R必在AB上,作AB边上的高CE,E在线段AB上,连接CR交AD于M,
∴MN=MR,
∴CM+MN=CM+MR=CR≥CE,
∵面积为8,AB=4,
∴8=
AB•BE,
∴BE=4,
∴MN+MC的最小值为4.
 解:设N关于AB的对称点为R,由于为锐角三角形,则R必在AB上,作AB边上的高CE,E在线段AB上,连接CR交AD于M,
解:设N关于AB的对称点为R,由于为锐角三角形,则R必在AB上,作AB边上的高CE,E在线段AB上,连接CR交AD于M,∴MN=MR,
∴CM+MN=CM+MR=CR≥CE,
∵面积为8,AB=4,
∴8=
| 1 |
| 2 |
∴BE=4,
∴MN+MC的最小值为4.
点评:本题考查了轴对称-最短路线问题,解题的关键是正确的作出对称点和利用垂直平分线的性质证明BM+MN的最小值为三角形某一边上的高线.

练习册系列答案
相关题目
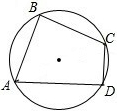 如图,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,则BC=
如图,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,则BC=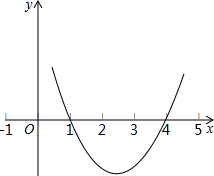 已知二次函数y=ax2-5x+c的图象如图所示.
已知二次函数y=ax2-5x+c的图象如图所示.