题目内容
1.在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出如表:| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y1 | … | 0 | -3 | -4 | -3 | 0 | … |
| y2 | … | 0 | 2 | 4 | 6 | 8 | … |
分析 先利用待定系数法求出二次函数与一次函数的解析式,求出两函数图象的交点坐标,进而根据两个函数图象在直角坐标系中的上下位置关系可得出结论.
解答 解:∵由题意得,$\left\{\begin{array}{l}{a-b+c=0}\\{c=-3}\\{a+b+c=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1\\;}\\{b=-2}\\{c=-3}\end{array}\right.$,
∴二次函数的解析式为y=x2-2x-3=(x-1)2-4,
∵一次函数y2=kx+m的图象过点(-1,0),(0,2),
∴$\left\{\begin{array}{l}{-k+m=0}\\{m=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=2}\\{m=2}\end{array}\right.$,
∴一次函数的解析式为y=2x+2,
如图所示,当-1<x<5时,二次函数的值小于一次函数的值.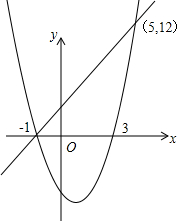
故答案为:-1<x<5.
点评 本题考查的是二次函数与不等式,能利用数形结合求出不等式的解集是解答此题的关键.利用两个函数图象在直角坐标系中的上下位置关系求自变量的取值范围,可作图利用交点直观求解,也可把两个函数解析式列成不等式求解.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
12.下列说法中,不正确的是( )
| A. | 同角的余角相等 | |
| B. | 两直线平行,同旁内角相等 | |
| C. | 在同一平面内,不相交的两条直线叫平行线 | |
| D. | 对顶角相等 |
6.在-$\frac{1}{2}$,-$\frac{1}{3}$,-2,-1这四个数中,最大的数是( )
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | -2 | D. | -1 |
13.已知等腰三角形一腰上的中线将它的周长分成9cm和12cm两部分,则等腰三角形的底边长为( )
| A. | 9cm | B. | 5cm | C. | 6cm或5cm | D. | 5cm或9cm |
10.某人去水果批发市场采购苹果,他看中了A、B两家苹果、这两家苹果品质一样,零售价都为10元/千克,批发价各不相同.
A家规定:批发数量不超过100千克,按零售价的90%优惠;批发数量不超过200千克,按零售价的80%优惠;超过200千克的按零售价的70%优惠.
B家的规定如表:
(1)如果他批发60千克苹果,则他在A、B两家批发分别需要多少元?
(2)如果他批发x千克苹果(150<x<200),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发180千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
A家规定:批发数量不超过100千克,按零售价的90%优惠;批发数量不超过200千克,按零售价的80%优惠;超过200千克的按零售价的70%优惠.
B家的规定如表:
| 数量范围(千克) | 0~50 | 50以上~150的部分 | 150以上~250的部分 | 250以上的部分 |
| 价格(元) | 零售价的90% | 零售价的80% | 零售价的70% | 零售价的60% |
(2)如果他批发x千克苹果(150<x<200),请你分别用含x的代数式表示他在A、B两家批发所需的费用;
(3)现在他要批发180千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
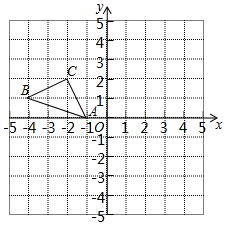 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: