��Ŀ����
16����ͼ��A��0��6����B��-6��0������C��Dͬʱ�ӵ�O��A������ÿ��1����λ���ٶȷֱ�����x�������������AO�����˶���ͬʱ��E�ӵ�B��������ÿ��2����λ��������BO�˶�������C��ֱ��l��x�ᣬ��F��ֱ��l��x���Ϸ���һ�㣬��EF=ED����DE��EFΪ�ڱ�������DEFG������C�͵�E�غ�ʱ����ͬʱֹͣ�˶���ֱ��m��y=2x+2��x���ڵ�M����y���ڵ�N�����˶�ʱ��Ϊt��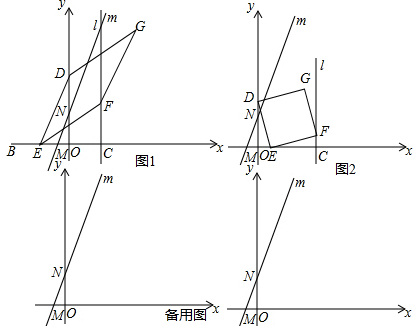
��1����ͼ1ֱ��д����M�͵�N�����겢��t�Ĵ���ʽ��ʾCE��OD�ij��ȣ�
M��-1��0����N��0��2����CE=6-t��OD=6-t����
��2����ͼ2������E���߶�OC֮��ʱ��֤��������DEFGΪ�����Σ�
��3���������˶������У�
�ٵ�t��ֵΪ����ʱ���ı���DEFG��һ����������ֱ��m�ϣ�
�ڼǵ�D����ֱ��m�ĶԳƵ�Ϊ��D�䣬����D��ǡ������ֱ��l��ʱ��ֱ��д��t��ֵ��$\frac{16}{9}$��
���� ��1�����ֱ��y=2x+2��������Ľ��㣬�ɵ�M��N�����꣬������OE=t��AD=t��BE=2t�������Ƴ�CE��OD�ij���
��2������һ������90��������������Σ�ֻҪ֤����DEF=90�㼴�ɣ�
��3���ٷ��������ηֱ����ۼ��ɣ�����ͼ5�У���DD�佻ֱ��m��F����FG��OA��G���ɡ�DFG�ס�FNG�ס�MNO����$\frac{DG}{FG}$=$\frac{FG}{GN}$=$\frac{OM}{ON}$=$\frac{1}{2}$���Ƴ�DG=$\frac{1}{4}$t��GN=t��
����GN=AN-AD-DG���г����̼��ɽ�����⣮
��� �⣺��1����y=2x+2��x���ڵ�M����y���ڵ�N��
��M��-1��0����N��0��2����
�����⣬OE=t��AD=t��BE=2t��
��EC=OB+OC-BE=6+t-2t=6-t��OD=OA-AD=6-t��
�ʴ�Ϊ��-1��0������0��2����6-t��6-t��
��2��֤������E���߶�OC֮��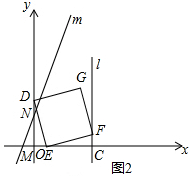
��CE=6-t=OD��EF=ED����DOE=��ECF=90�㣮
���DOE�ա�ECF
���DEO=��EFC
���DEO+��CEF=��EFC+��CEF=90�㣬
���DEF=90��
������DEFG��������
��3���ٵ���D����ֱ��m�ϣ�����D���N�غϣ�
�ɵ�6-t=2
��t=4��
����E����ֱ��m�ϣ�����E���M�غϣ�
�ɵ�2t=5
��t=2.5��
����F����ֱ��m�ϣ���ͼ3��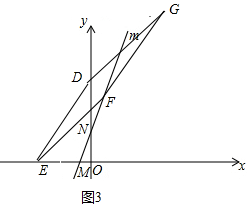
�ɡ�DOE�ա�FCE
�ɵ�CF=OE=6-2t
��F �� t��6-2t ������y=2x+2
6-2t=2t+2
��t=1��
����G����ֱ��m�ϣ���ͼ4��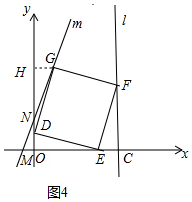
��G��GH��x���ڵ�H
����֤����DOE�ա�GHD��
��GH=OD=6-t��HD=OE=2t-6
��OH=HD+OD=t
��G ��6-t��t ������y=2x+2
t=2��6-t��+2��t=$\frac{14}{3}$��
�൱tȡ4��2.5��1��$\frac{14}{3}$ʱ���ı���DEFG��һ����������ֱ��m��
����ͼ5�У���DD�佻ֱ��m��F����FG��OA��G��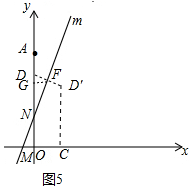
�����⣬D����ֱ��m�ĶԳƵ�Ϊ��D�䣬����D��ǡ������ֱ��l�ϣ�
��FG=$\frac{t}{2}$��AD=t��
�ɡ�DFG�ס�FNG�ס�MNO��
��$\frac{DG}{FG}$=$\frac{FG}{GN}$=$\frac{OM}{ON}$=$\frac{1}{2}$��
��DG=$\frac{1}{4}$t��GN=t��
��GN=AN-AD-DG��
��t=4-t-$\frac{1}{4}$t��
��t=$\frac{16}{9}$��
��t=$\frac{16}{9}$ʱ��D����ֱ��m�ĶԳƵ�Ϊ��D�䣬����D��ǡ������ֱ��l�ϣ�
���� ���⿼��һ�κ����ۺ��⡢ȫ�������� ���ж������ʣ����������ε��ж������������ε��ж������ʣ�����Ĺؼ������������ѧ֪ʶ��ѧ���÷������۵�˼��˼�����⣬ѧ�����ӳ��ø����ߣ��������������ν�����⣬�����п�ѹ���⣮

 ��������������������ϵ�д�
��������������������ϵ�д�| ����Ĵ���s | 150 | 300 | 600 | 900 | 1200 | 1500 |
| ���������Ƶ��n | 63 | a | 247 | 365 | 484 | 606 |
| ���������Ƶ��$\frac{n}{s}$ | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
��2������ƣ�������s�ܴ�ʱ�����������Ƶ�ʽ���ӽ�0.4��
��3�������㣺��������ĸ�����0.6����ȷ��0.1����
��4���Թ��㣺�ڴ��к����ж���ֻ��
��5�����������4������������ͳ������ʷ���̸һ����ʾ��
| x | �� | -1 | 0 | 1 | 2 | 3 | �� |
| y1 | �� | 0 | -3 | -4 | -3 | 0 | �� |
| y2 | �� | 0 | 2 | 4 | 6 | 8 | �� |
 �������Ϸֱ���A��B��C��D����A��ʾ��$\frac{1}{3}$����B��ʾ��1$\frac{1}{2}$����C��ʾ��-2����D��ʾ��2$\frac{3}{4}$��������A��B��C��D����ʾ�����á��������ӣ�
�������Ϸֱ���A��B��C��D����A��ʾ��$\frac{1}{3}$����B��ʾ��1$\frac{1}{2}$����C��ʾ��-2����D��ʾ��2$\frac{3}{4}$��������A��B��C��D����ʾ�����á��������ӣ�