题目内容
19.已知直线y=x+3与反比例函数y=$\frac{-{k}^{2}}{x}$的图象相交于点A(x1,y1)、B(x2,y2),当y1+y2=3k时,求反比例函数的解析式.分析 由y=x+3得x=y-3,代入反比例函数解析式,即可得到一个关于y的方程,利用一元二次方程中根与系数的关系即可求解.
解答 解:由y=x+3得x=y-3,代入y=$\frac{-{k}^{2}}{x}$得:y=$\frac{-{k}^{2}}{y-3}$,
则y2-3y+k2=0.
则y1+y2=3=3k,
解得:k=1.
点评 本题考查了反比例函数与一次函数的交点,以及一元二次方程根与系数的关系,正确转化为根与系数的关系是关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
7.下列说法中错误的是( )
| A. | 不等式x<2的正整数解只有一个 | B. | x<$\frac{1}{2}$是不等式2x-1<0的解集 | ||
| C. | 不等式ax>9的解集是x>$\frac{9}{a}$ | D. | 不等式x<10的整数解有无数个 |
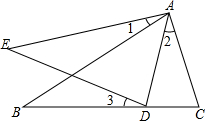 如图,已知∠1=∠2=∠3,ED=BC,试判断△ACD的形状,并说明理由.
如图,已知∠1=∠2=∠3,ED=BC,试判断△ACD的形状,并说明理由. 如图,正比例函数图象经过点A,将该图象向下平移2个单位后函数解析式是y=3x-2.
如图,正比例函数图象经过点A,将该图象向下平移2个单位后函数解析式是y=3x-2.