题目内容
16.关于x的一元二次方程x2-mx+5(m-5)=0的两个正实数根分别为x1,x2,且2x1+x2=7,则m的值是6.分析 根据根与系数的关系得到x1+x2=m,x1•x2=5(m-5),由于2x1+x2=7,则可解出x1=7-m,x2=2m-7,所以(7-m)(2m-7)=5(m-5),解得m1=2,m2=6,然后根据x1,x2为正实数可确定m的值为6.
解答 解:根据题意得x1+x2=m,x1•x2=5(m-5),
∵2x1+x2=7,
∴x1=7-m,x2=2m-7,
∴(7-m)(2m-7)=5(m-5),
整理得m2-8m+12=0,解得m1=2,m2=6,
∵x1,x2为正实数,
∴m>5,
∴m的值为6.
故答案为6.
点评 若本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
7.下列说法中错误的是( )
| A. | 不等式x<2的正整数解只有一个 | B. | x<$\frac{1}{2}$是不等式2x-1<0的解集 | ||
| C. | 不等式ax>9的解集是x>$\frac{9}{a}$ | D. | 不等式x<10的整数解有无数个 |
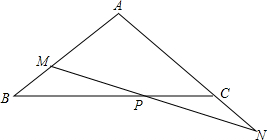 如图,已知在△ABC中,AB=AC,P是BC边上的-点,过点P引直线分别交AB于点M,交AC的延长线于点N,且PM=PN.
如图,已知在△ABC中,AB=AC,P是BC边上的-点,过点P引直线分别交AB于点M,交AC的延长线于点N,且PM=PN. 已知,如图,在矩形ABCD中,AC,BD相交于点O,E为AD的中点,连结EO并延长,交BC于F,求证:CF=BF.
已知,如图,在矩形ABCD中,AC,BD相交于点O,E为AD的中点,连结EO并延长,交BC于F,求证:CF=BF. 如图是一个风筝设计图,其中AB=BC,AD=CD,AC,BD交于点O,请判断AC与BD是否互相垂直,并说明理由.
如图是一个风筝设计图,其中AB=BC,AD=CD,AC,BD交于点O,请判断AC与BD是否互相垂直,并说明理由.