题目内容
16.等腰直角△ABC中,∠BAC=90°,AB=AC,点A、点B分别是x轴、y轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;(1)如图1,若A(0,2),B(4,0),D(-1,0),过点C作AC的垂线交y轴于点F,求点F的坐标;
(2)如图2,调整等腰直角△ABC位置,使点D恰为AC中点,连接DE,求证:∠ADB=∠CDE.

分析 (1)由直角三角形的性质和角的互余关系证出∠CAF=∠ABD,由ASA证明△ACF≌△BAD,得出AF=BD,求出OF,即可得出结果;
(2)作CF⊥AC交y轴于F,先证明△ACF≌△BAD,得到AD=CF,∠AFC=∠ADB,再证明△CDE≌△CFE,得到∠CDE=∠CFE,即可得出结论.
解答 (1)解:∵A(0,2),B(4,0),D(-1,0),
∴OA=1,OB=4,OD=1,
∵∠BAC=90°,∠AOB=90°,
∴∠CAF+∠BAO=90°,∠BAO+∠ABD=90°,
∴∠CAF=∠ABD,
∵CF⊥AC,
∴∠ACF=90°=∠BAD,
在△ACF和△BAD中,$\left\{\begin{array}{l}{∠CAF=∠ABD}&{\;}\\{AC=BA}&{\;}\\{∠ACF=∠BAD}&{\;}\end{array}\right.$,
∴△ACF≌△BAD(ASA),
∴AF=BD=OD+OB=1+4=5,
∴OF=AF-OA=5-2=3,
∴点F的坐标为(0,-3);
(2)证明:作CF⊥AC交y轴于F,如图所示:
由(1)可得∠CAF=∠ABD,
在△ACF和△BAD中,$\left\{\begin{array}{l}{∠CAF=∠ABD}&{\;}\\{AC=BA}&{\;}\\{∠ACF=∠BAD}&{\;}\end{array}\right.$,
∴△ACF≌△BAD(ASA),
∴AD=CF,∠AFC=∠ADB,
∵点D为AC中点,
∴AD=CD,
∴CD=CF,
∵∠ACB=45°,
∴∠FCE=45°,
在△CDE和△CFFE中,$\left\{\begin{array}{l}{CD=CF}&{\;}\\{∠DCE=∠FCE}&{\;}\\{CE=CE}&{\;}\end{array}\right.$,
∴△CDE≌△CFE(SAS),
∴∠CDE=∠AFC,
∴∠ADB=∠CDE.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的性质、坐标与图形性质、直角三角形的性质;熟练掌握等腰直角三角形的性质,证明三角形全等是解决问题的关键.

| A. | 在直角三角形中,30°角所对的直角边y与斜边x之间的关系 | |
| B. | 在等腰三角形中,顶角y与底角x之间的关系 | |
| C. | 圆的面积S与它的直径d之间的关系 | |
| D. | 面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系 |
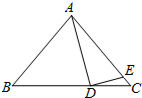 如图,在△ABC中,AB=AC,点D是BC上一点,点E是AC上一点,且DE⊥AD.若∠BAD=55°,∠B=50°,求∠DEC的度数.
如图,在△ABC中,AB=AC,点D是BC上一点,点E是AC上一点,且DE⊥AD.若∠BAD=55°,∠B=50°,求∠DEC的度数.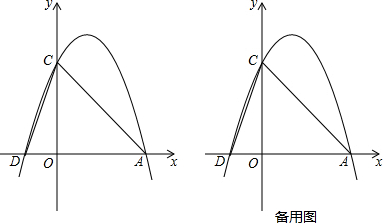
 如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点.
如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,D为抛物线的顶点.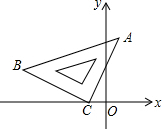 在平面直角坐标系中,将一块等腰三角板ABC如图放置.已知直角顶点C的坐标为(-2,0),顶点B的坐标为(-7,3).求点A的坐标.
在平面直角坐标系中,将一块等腰三角板ABC如图放置.已知直角顶点C的坐标为(-2,0),顶点B的坐标为(-7,3).求点A的坐标.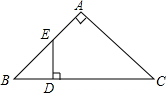 如图,在Rt△ABC中,∠A=90°,D为BC上一点,DC=AC,过点D作DE⊥BC交AB于点E,从图中找出与DE相等的线段,并证明.
如图,在Rt△ABC中,∠A=90°,D为BC上一点,DC=AC,过点D作DE⊥BC交AB于点E,从图中找出与DE相等的线段,并证明.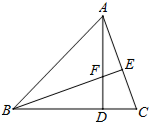 如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为3.
如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为3.