题目内容
10. 如图所示,AB+CD<AC+BD.(填“<”,“>”或“=”)
如图所示,AB+CD<AC+BD.(填“<”,“>”或“=”)
分析 AC与BD的交点为E,由两点之间线段最短可知AE+BE>AB,同理得到CE+DE>DC,从而得到AB+CD<AC+BD.
解答 解:如图所示:
由两点之间线段最短可知AE+BE>AB.
同理:CE+DE>DC.
∴AE+BE+CE+DE>AB+DC.
∴AC+BD>AB+DC,即AB+DC<AC+BD.
故答案为:<.
点评 本题主要考查的是线段的性质,掌握线段的性质是解题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
15.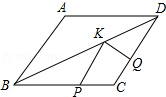 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
2. 如图,为了测量某栋大楼的高度AB,在D处用高为1米的测角仪CD测得大楼顶端A的仰角为30°,向大楼方向前进100米到达F处,又测得大楼顶端A的仰角为60°,则这栋大楼的高度AB(单位:米)为( )
如图,为了测量某栋大楼的高度AB,在D处用高为1米的测角仪CD测得大楼顶端A的仰角为30°,向大楼方向前进100米到达F处,又测得大楼顶端A的仰角为60°,则这栋大楼的高度AB(单位:米)为( )
 如图,为了测量某栋大楼的高度AB,在D处用高为1米的测角仪CD测得大楼顶端A的仰角为30°,向大楼方向前进100米到达F处,又测得大楼顶端A的仰角为60°,则这栋大楼的高度AB(单位:米)为( )
如图,为了测量某栋大楼的高度AB,在D处用高为1米的测角仪CD测得大楼顶端A的仰角为30°,向大楼方向前进100米到达F处,又测得大楼顶端A的仰角为60°,则这栋大楼的高度AB(单位:米)为( )| A. | $50\sqrt{3}+1$ | B. | $50\sqrt{3}$ | C. | 51 | D. | 101 |
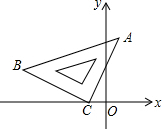 在平面直角坐标系中,将一块等腰三角板ABC如图放置.已知直角顶点C的坐标为(-2,0),顶点B的坐标为(-7,3).求点A的坐标.
在平面直角坐标系中,将一块等腰三角板ABC如图放置.已知直角顶点C的坐标为(-2,0),顶点B的坐标为(-7,3).求点A的坐标.
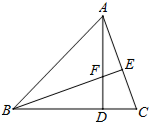 如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为3.
如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为3.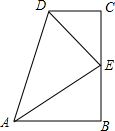 如图,四边形ABCD中,∠B=∠C=90°,∠CED=35°,DE平分∠ADC.
如图,四边形ABCD中,∠B=∠C=90°,∠CED=35°,DE平分∠ADC.