题目内容
对于任意实数k,方程x2-kx+k-1=0的根的情况是 .
考点:根的判别式
专题:
分析:判断上述方程的根的情况,只要看根的判别式b2-4ac的值的符号就可以了.
解答:解:∵a=1,b=-k,c=k-1,
∴b2-4ac
=(-k)2-4×1×(k-1)
=k2-4k+4
=(k-2)2,
无论k取什么数值,(k-2)2≥0,
∴方程x2-kx+k-1=0都有两个实数根.
故答案为:有两个实数根.
∴b2-4ac
=(-k)2-4×1×(k-1)
=k2-4k+4
=(k-2)2,
无论k取什么数值,(k-2)2≥0,
∴方程x2-kx+k-1=0都有两个实数根.
故答案为:有两个实数根.
点评:一元二次方程根的情况与判别式△的关系:(1)b2-4ac>0?方程有两个不相等的实数根;(2)b2-4ac=0?方程有两个相等的实数根;(3)b2-4ac<0?方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
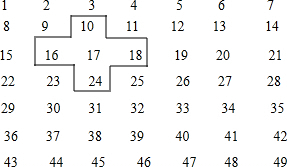 如图是一张按一定顺序排列的自然数表,用一个有五个空格的十字框可以框出五个数字,现框出的五个数字中,四个角上的数字分别是10、16、18、24.如果框出的四个角上的四个数字之和为132,那么,被框出的五个数字分别是
如图是一张按一定顺序排列的自然数表,用一个有五个空格的十字框可以框出五个数字,现框出的五个数字中,四个角上的数字分别是10、16、18、24.如果框出的四个角上的四个数字之和为132,那么,被框出的五个数字分别是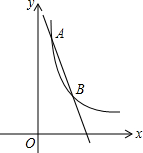 如图,一次函数y=kx+b与反比例函数
如图,一次函数y=kx+b与反比例函数 如图,梯形ABCD中,F是CD的中点,AF⊥AB,E是BC边上是一点,且AF平分∠DAE.若EF=5,则AB=
如图,梯形ABCD中,F是CD的中点,AF⊥AB,E是BC边上是一点,且AF平分∠DAE.若EF=5,则AB= 如图,已知正方形ABCD,延长AB到E,作AG⊥EC于G,AG交BC于F,求证:AF=CE.
如图,已知正方形ABCD,延长AB到E,作AG⊥EC于G,AG交BC于F,求证:AF=CE.