题目内容
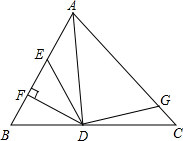 如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和40,则△EDF的面积为
如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和40,则△EDF的面积为考点:角平分线的性质
专题:
分析:过点D作DH⊥AC于H,根据角平分线上的点到角的两边距离相等可得DF=DH,然后利用“HL”证明Rt△DEF和Rt△DGH全等,根据全等三角形的面积相等可得S△EDF=S△GDH,设面积为S,然后根据S△ADF=S△ADH列出方程求解即可.
解答: 解:如图,过点D作DH⊥AC于H,
解:如图,过点D作DH⊥AC于H,
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DH,
在Rt△DEF和Rt△DGH中,
,
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH,设面积为S,
同理Rt△ADF≌Rt△ADH,
∴S△ADF=S△ADH,
即40+S=50-S,
解得S=5.
故答案为:5.
 解:如图,过点D作DH⊥AC于H,
解:如图,过点D作DH⊥AC于H,∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DH,
在Rt△DEF和Rt△DGH中,
|
∴Rt△DEF≌Rt△DGH(HL),
∴S△EDF=S△GDH,设面积为S,
同理Rt△ADF≌Rt△ADH,
∴S△ADF=S△ADH,
即40+S=50-S,
解得S=5.
故答案为:5.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,作辅助线构造出全等三角形并利用角平分线的性质是解题的关键.

练习册系列答案
相关题目
下列说法,正确的是( )
| A、若|a|=-a,则a<0 | ||||
| B、若|a|=|b|=2,则a=2,b=±2 | ||||
C、若a=b,m为有理数,则
| ||||
| D、若a<0,b>0,则ab<0 |
下列各命题中,其逆命题是真命题的是( )
| A、全等三角形的三个角分别对应相等 |
| B、全等三角形的面积相等 |
| C、线段垂直平分线上的点到这条线段两个端点的距离相等 |
| D、如果a、b都是正数,那么他们的积ab也是正数 |
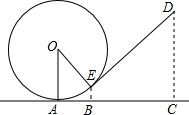 如图是小朋友玩的“滚铁环”游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A,若⊙O的半径为25cm,cos∠AOE=
如图是小朋友玩的“滚铁环”游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A,若⊙O的半径为25cm,cos∠AOE= 如图,AB是⊙O的直径,∠C=40°,则∠ABD=
如图,AB是⊙O的直径,∠C=40°,则∠ABD=